hãy vẽ hình theo ký hiệu sau
A thuôc p
A thuộc q
B thuộc q
B thuộc p
Cho tứ diện ABCD. Gọi M, N là trung điểm AB, CD; P,Q là hai điểm theo thứ tự thuộc hai cạnh AC, BD sao cho PA/PC=QB/QD. Chứng minh rằng M, N, P, Q cùng thuộc một mặt phẳng.
a) Cho A = 5a+3b; B = 13a+8b(a; b thuộc N*)chứng minh (A; B) = (a; b)
b) Tổng quát A = ma + nb; B = pa + qb thỏa mãn |mq - np| = 1 với a; b; m; n; p; q thuộc N*. Chứng minh (A; B) = (a; b)
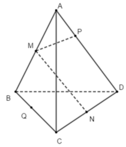
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho P A → = m P D → và Q B → = m Q C → , với m khác 1. Vecto M P → bằng:
A. M B → − m Q C →
B. M N → − m P D →
C. M A → − m P D →
D. M N → − m Q C →
Có thể loại các phương án A, B và D vì các cặp ba vecto ( M P → , M B → , v à Q C → ) , ( M P → , M N → , P D → ) và ( M P → , M N → v à Q C → ) đều không đồng phẳng.
Phương án C đúng vì : M P → = M A → + A P → = M A → - m P D →
Đáp án C
Cho tập hợp A = { 3,9 } , hãy điền ký hiệu thuộc , không thuộc .
a. 3
cho đường thẳng, diểm A thuộc dường thẳng a
Điểm B không thuộc đường thẳng â) vẽ hình và viết kí hiệu
a) vẽ hình và viết kí hiệu
b) có điểm nào khác điểm A mà thuộc đường thẳng a hay không?
Hãy vẽ hai điểm như thế và kí hiệu
c) có điểm nào khác điểm B mà không thuộc đường thẳng a hay không
Hãy vẽ hai điểm như thế và kí hiệu
a) \(A\in m;B\in m\)
b)Có những điểm khác điểm A cũng thuộc đường thẳng m chẳng hạn hai điểm C và D
Vẽ kí hiệu
\(C\in m;D\in m\)
c) Có những điêrm khác thuộc điểm m chẳng hạn hai điểm M và N M \(\in\) N\(\notin\) n
~Study well~ :)
Vẽ hình theo các kí hiệu sau:
A thuộc p ; B không thuộc q.
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Cho tam giác EQB , góc E = 900 . Kẻ EI vuông góc QB ( I thuộc QB ) ; IH vuông góc EB ( H thuộc EB )
a) Vì sao EQ // IH ?
b) góc Q = 600 . Tính góc EIH , góc QEI
Cho tam giác EQB , góc E = 900 . Kẻ EI vuông góc QB ( I thuộc QB ) ; IH vuông góc EB ( H thuộc EB )
a) Vì sao EQ // IH ?
b) góc Q = 600 . Tính góc EIH , góc QEI .
a) IHB = E = 90* ( 2 góc đồng vị)
=> HI // EQ
b) E + Q + B = 180* ( tổng 3 góc tam giác )
90* + 60* + B = 180*
150* + B = 180*
B = 180* - 150* = 30*
Vẽ thêm tia IK // HB sao cho IB nằm giữa 2 tia IH và IK
IK // HB
=>KIB = B = 30*
IK // HB => IK vuông góc IH
IH vuông góc EB
KIB + BIH = KIH
30* + BIH = 90*
BIH = 90* - 30* = 60*
EIH + BIH = EIB
EIH + 60* = 90*
EIH = 90* -60* =30*
EQ // IH
=> QEI = EIH = 30* ( 2 góc so le trong )
Câu 4: (2,5 điểm )Cho tam giác ABC có K là trung điểm của AC. Qua K kẻ KM//BC
(M thuộc cạnh AB), KP//AB (P thuộc BC)
a)Chứng minh rằng tứ giác MKPB là hình bình hành và P là trung điểm BC
b)Gọi Q đối xứng với P qua M. Chứng minh QB//AP
c)Gọi I là trung điểm QB và O là giao điểm của AP và MK.
Chứng minh I,O,K thẳng hàng.