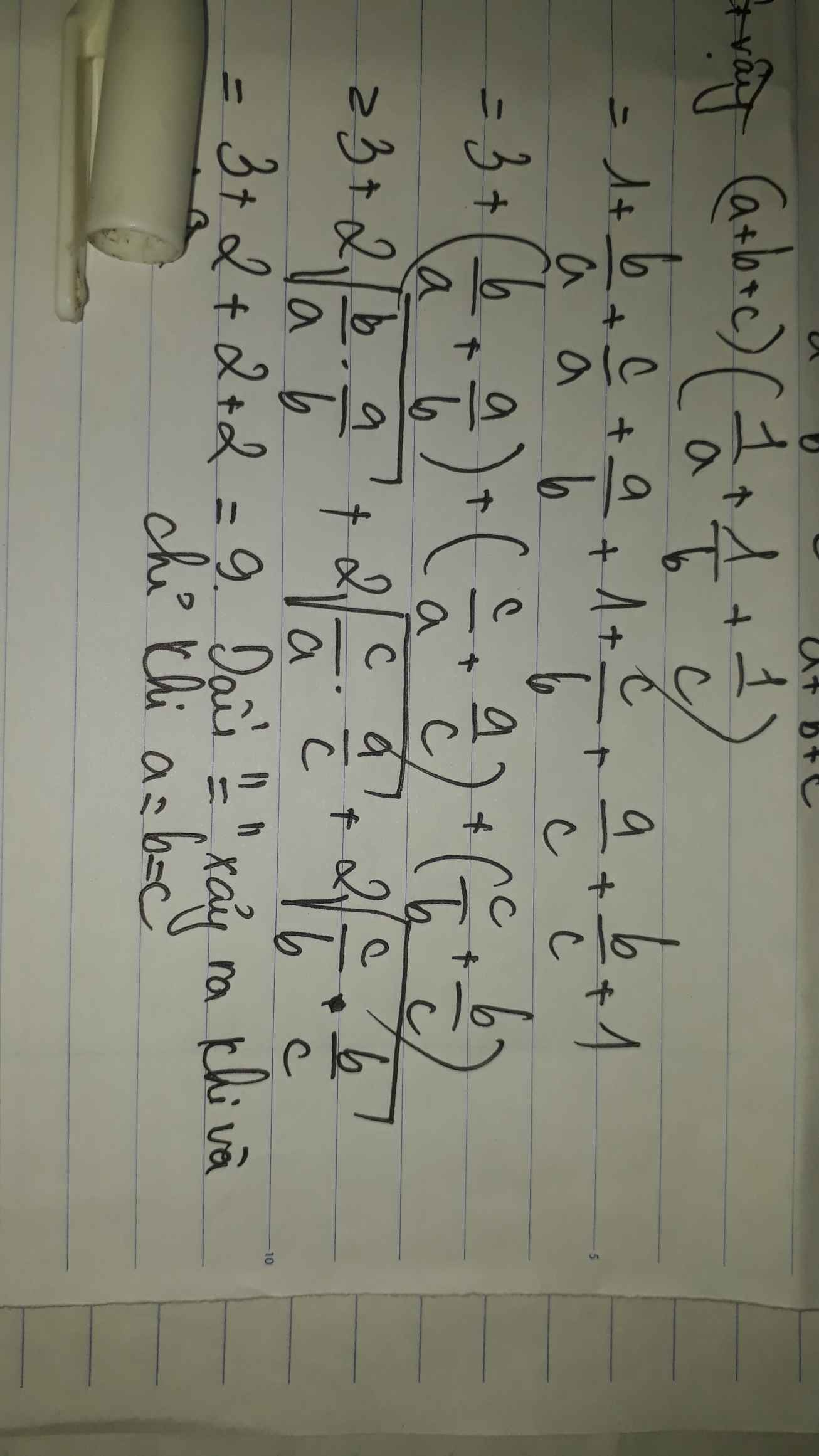Chứng minh: (1+1/a)(1+1/b) ≥ 9 với a+b=1.

Những câu hỏi liên quan
Với a,b,c là các số dương. Chứng minh (a+b+c)(\(\dfrac{1}{a}\)+\(\dfrac{1}{b}\)+\(\dfrac{1}{c}\))≥9
Chứng minh: Với a; b; c dương (a+b+c)(1/a+1/b+1/c) lớn hơn hoặc bằng 9
Chứng minh đẳng thức:a)
a
2
−
3
a
a
2
+
9
−
6
a
2...
Đọc tiếp
Chứng minh đẳng thức:
a) a 2 − 3 a a 2 + 9 − 6 a 2 27 − 9 a + 3 a 2 − a 3 . 1 − 2 a − 3 a 2 = a + 1 a với a ≠ 0 ; 3 ;
b) 2 5 b − 2 b + 1 . b + 1 5 b − 3 5 b − 3 5 : b − 1 b = 6 b 5 ( b − 1 ) với b ≠ 0 ; ± 1 .
Thực hiện phép tính đối với vế trái của mỗi đẳng thức.
Đúng 0
Bình luận (0)
Chứng minh bất đăng thức luôn đúng với mọi a,b,c
1/a +1/b +1/c ≥ 9/a+b+c
Áp dụng bđt AM-GM ta có:
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\)
\(a+b+c\ge3\sqrt[3]{abc}\)
Nhân 2 vế của đẳng thức trên ta được:
\(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{9}{a+b+c}\)
Áp dụng BDT svacxo ta có:
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{\left(1+1+1\right)^2}{a+b+c}=\frac{9}{a+b+c}\)
Dấu = khi a=b=c
Học tốt
Trả lời :
- Hai bn kia làm đúng
- Chúc học tốt
- Tk cho mk nha
cho a/b = 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9 với a;b thuộc N. Chứng minh rằng a chia hết cho 11.
chứng minh rằng
1/a + 1/b +1/c >= 9 với mọi a , b , c>0 và a+b+c=1
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{a+b+c}{a}+\frac{a+b+c}{b}+\frac{a+b+c}{c}=1+\frac{b}{a}+\frac{c}{a}+1+\frac{a}{b}+\frac{c}{b}+1+\frac{a}{c}+\frac{b}{c}.\)
\(=3+\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)\)
Theo Cosy với a;b;c >0
\(\frac{a}{b}+\frac{b}{a}\ge2\sqrt{\frac{a}{b}\cdot\frac{b}{a}}=2\);\(\frac{b}{c}+\frac{c}{b}\ge2\sqrt{\frac{b}{c}\cdot\frac{c}{b}}=2\);\(\frac{a}{c}+\frac{c}{a}\ge2\sqrt{\frac{a}{c}\cdot\frac{c}{a}}=2\)
Do đó: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3+2+2+2=9\)đpcm.
Dấu "=" khi a=b=c=1/3.
Đúng 1
Bình luận (0)
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 0Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| |a + b|Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| |a − b|Bài 8. Chứng minh rằng: |x − 1| + |x − 2| 1Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| 2Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| 4Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| 2
Đọc tiếp
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 =0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| < |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 0Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| |a + b|Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|Bài 8. Chứng minh rằng: |x − 1| + |x − 2| 1Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| 2Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| 4Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| 2
Đọc tiếp
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)
2 = 0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
9. a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh : (a + 1)(b + 1)(c + 1) ≥ 8
a, \(\left(a+1\right)^2\ge4a\)
\(\Leftrightarrow a^2+2a+1\ge4a\)
\(\Leftrightarrow a^2-2a+1\ge0\)
\(\Leftrightarrow\left(a-1\right)^2\ge0\)(Luôn đúng)
b, Áp dụng bđt Cô-si
\(a+1\ge2\sqrt{a}\)
\(b+1\ge2\sqrt{b}\)
\(c+1\ge2\sqrt{c}\)
\(\Rightarrow\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
\(=8\sqrt{abc}=8\)(ĐPCM)
Dấu "=" khi a = b = c =1
Đúng 0
Bình luận (0)
a, \(\left(a-1\right)^2\ge0\)
\(\Rightarrow a^2-2a+1\ge0\)
\(\Leftrightarrow a^2+2a+1>4a\)
\(\Leftrightarrow\left(a+1\right)^2\ge4a.\)
b, Áp dụng bất đẳng thức trên ta có :
( a + 1 )2 > 4a \(\Leftrightarrow\) \(\sqrt{\left(a+1\right)^2}\ge2\sqrt{a}\)
mà \(\sqrt{\left(a+1\right)^2}=\left|a+1\right|\)
Do a > 0 nên a + 1 > 0. Vậy | a + 1 | = a + 1.
Khi đó : a + 1 > \(2\sqrt{a}\)
Tương tự ta có :
b + 1 > \(2\sqrt{b}\)và c + 1 > \(2\sqrt{c}\)
=> ( a + 1 ) ( b + 1 ) ( c + 1 ) > \(8\sqrt{abc}=8.\)
Đúng 0
Bình luận (0)