cho tứ giác abcd ngoại tiếp đường tròn tâm i thõa mãn (ai+di)^2 + (bi + ci)^2 = (ab+cd)^2 cmr abcd là hình thang cân

Những câu hỏi liên quan
Cho tứ giác ABCD ngoại tiếp đường tròn tâm I thỏa mãn :
\(\left(AI+DI\right)^2+\left(BI+CI\right)^2=\left(AB+CD\right)^2\)
Chứng minh rằng ABCD là hình thang cân .
Cho hình thang cân ABCD đáy bé AD. ABCD ngoại tiếp đường tròn bán kính bằng 1 và nội tiếp đường tròn tâm O. Gọi P là trung điểm AB thỏa mãn OP=4. Tính diện tích ABCD
Xem chi tiết
Cho hình thang ABCD (AB//CD), có BD^2=AB.CD. CMR: Đường tròn ngoại tiếp tam giác ABD tiếp xúc với BC.
cho hình thang cân abcd (ab//cd;ab<cd) ngoại tiếp đg tròn (O;R).CMR: ab.cd=ur^2
cho hình thang cân abcd (ab//cd;ab<cd) ngoại tiếp đg tròn (O;R).CMR: ab.cd=ur^2
cho hình thang ABCD ( AB //CD)
Có : BD^2 = AB.CD
CMR : Đường tròn ngoại tiếp tam giác ABD tiếp xúc với BC
Cho đường tròn tâm O và tứ giác ABCD nội tiếp đường tròn tâm O có 2 đường chéo AC và BD vuông góc với nhau. Vẽ đường kính BK của đường tròn tâm O.
a) Chứng minh: tứ giác ACKD là hình thang cân
b)\(AB^2+BC^2+CD^2+DA^2=8R^2\)
(mình chỉ mới hc tới liên hệ giữa dây và khoảng cách từ tâm đến dây th nhé)
Cho hình thang cân ABCD nội tiếp đường tròn (O) với AB song song CD và ABCD.M là trung điểm CD. P là điểm di chuyển trên đoạn MD ( P khác M, D ).AP cắt (O) tại Q khác A, BP cắt (O) tại R khác B, QR cắt CD tại E. Gọi F là điểm đối xứng với P qua E1) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác AQF luôn thuộc một đường thẳng cố định khi P di chuyển.
Đọc tiếp
Cho hình thang cân ABCD nội tiếp đường tròn (O) với AB song song CD và AB<CD.
M là trung điểm CD. P là điểm di chuyển trên đoạn MD ( P khác M, D ).
AP cắt (O) tại Q khác A, BP cắt (O) tại R khác B, QR cắt CD tại E. Gọi F là điểm đối xứng với P qua E
1) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác AQF luôn thuộc một đường thẳng cố định khi P di chuyển.
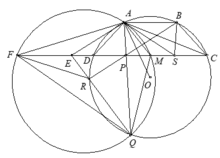
1). Gọi S điểm đối xứng với P qua M.Theo tính chất đối xứng của hình thang cân dễ thấy tứ giác ABSP cũng là hình thang cân.
Ta lại có Q P S ^ = Q A B ^ = Q R B ^ .
Từ đó có E P Q ^ = E R P ^ ⇒ Δ E R P ∽ Δ E P Q (g – g),
nên E Q P ^ = E P R ^ = B P S ^ = A S E ^ , suy ra tứ giác AEQS nội tiếp.
Do đó P A . P Q = P E . P S = P F 2 .2 P M = P F . P M , suy ra tứ giác A M Q F nội tiếp.
Từ đó suy ra đường tròn ngoại tiếp tam giác △ A Q F luôn đi qua M.
Đúng 0
Bình luận (0)
a) AE và DE là hai tiếp tuyến nên AE┴AO; DE┴DO tứ giác EDOA nội tiếp đường tròn đường kính OE (1). Hình Thang ABCD cân ADBC hai cung tương ứng bằng nhau ^BDC^ACD 1/2 số đo cung nhỏ AD. ^DIA^IDC+^ICD (góc ngoài ∆DIC). ^DIA 2 lần ^ICD số đo cung nhỏ AD ^DOA Tứ giác AOID nội tiếp (I và O cùng nhìn AD với góc bằng nhau) (2) (1)&(2) 5 điểm A,E,D,I,O cùng nằm trên đường tròn đường kính OE hay tứ giác AEDI nội tiếp. b) ^BDC^ACD (cmt) ∆DIC cân đường trung trực của DC đi qua I. mà DC là một dây c...
Đọc tiếp
a) AE và DE là hai tiếp tuyến nên AE┴AO; DE┴DO => tứ giác EDOA nội tiếp đường tròn đường kính OE (1).
Hình Thang ABCD cân => AD=BC => hai cung tương ứng bằng nhau =>^BDC=^ACD = 1/2 số đo cung nhỏ AD.
^DIA=^IDC+^ICD (góc ngoài ∆DIC).
=>^DIA = 2 lần ^ICD = số đo cung nhỏ AD =^DOA => Tứ giác AOID nội tiếp (I và O cùng nhìn AD với góc bằng nhau) (2)
(1)&(2) => 5 điểm A,E,D,I,O cùng nằm trên đường tròn đường kính OE hay tứ giác AEDI nội tiếp.
b)
^BDC=^ACD (cmt) =>∆DIC cân =>đường trung trực của DC đi qua I. mà DC là một dây cung của (O) nên đường trung trực này cũng đi qua O => IO ┴ CD (3).
I nằm trên đường tròn đường kính OE (cmt) nên ^OIE=90° (góc nội tiếp chắn nửa đường tròn). =>EI ┴ OI (4).
(3)&(4)=> EI//DC hay EI//AB (vì AB//CD).
c)
Do RS//AB//DC nên áp dụng định lý Talét ta có CI/CA=DI/DB.
Trong ∆ADB ta có IR/AB=DI/DB.
Trong ∆ACB ta có IS/AB=CI/CA.
=>IR/AB=IS/AB => IR=IS hay I là trung điểm của RS.
d)
Xét ∆DAC ta có IR/DC=AI/CA
theo cmt ta có IR/AB=DI/DB=CI/CA
=>IR/DC+IR/AB=AI/CA+CI/CA=(AI+CI)/CA=1
=>IR/DC+IR/AB=1 Chia 2 vế chi IR ta có
=>1/DC+1/AB=1/IR
Mà RS=2.IR =>1/DC+1/AB=2/RS.
bạn nguyễn minh tâm ra nhận










