Chứng minh rằng : nếu ba số a;a+k ; a+2k nguyên tố lớn hơn 3 thì k chia hết cho 6

Những câu hỏi liên quan
Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng nếu
A
B
→
p
A
C
→
t
h
ì
A
B
→
p...
Đọc tiếp
Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng nếu A B → = p A C → t h ì A ' B ' → = p A ' C ' → , trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A’ và C’.
Để ý rằng
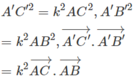
Ta có:
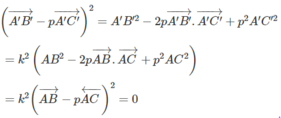
Từ đó suy ra 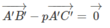
Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó A B → = t A C → , với 0 < t < 1. Áp dụng bài 1.39 ta cũng có A ' B → = t A ' C ' → , với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
Đúng 0
Bình luận (0)
Chứng minh rằng nếu ba số a, a+k, a+2k đều là các số nguyên tố lớn hơn 3, thì k chia hết cho 6
Do a, a + k, a + 2k đều là nguyên tố lớn hơn 3 nên đều là số lẻ và không chia hết cho 3.
• Vì a và a + k cùng lẻ nên a + k - a = k ⋮ 2. (1)
• Vì a, a + k, a + 2k đều không chia hết cho 3 nên khi chia cho 3 ít nhất hai số có cùng số dư, khi đó:
+ Nếu a và a + k có cùng số dư, thì suy ra: (a+k) - a = k ⋮ 3
+ Nếu a + k và a + 2k có cùng số dư, thì suy ra: (a+2k )- (a+k)= k ⋮ 3+ Nếu a và a + 2k có cùng số dư, thì suy ra:
( a + 2k ) - a = 2k 3 nhưng (2,3) = 1 nên k 3
Vậy, ta luôn có k chia hết cho 3 (2)
Từ (1),(2) và do (2,3)=1 ta suy ra k ⋮ 6, đpcm.
Nhận xét: Trong lời giải trên, ta đã định hướng được rằng để chứng minh k ⋮ 6 thì cần chứng minh k ⋮ 2 và k ⋮ 3 và ở đó:
• Việc chứng minh k ⋮ 2 được đánh giá thông qua nhận định a, a + k,a + 2k đều là nguyên tố lẻ hơn kém nhau k đơn vị.
• Việc chứng minh k ⋮ 3 được đánh giá thông qua nhận định “ba số lẻ không chia hết cho 3 thì có ít nhất hai số có cùng số dư” và như vậy hiệu của hai số đó sẽ chia hết cho 3.
Đúng 1
Bình luận (0)
Bạn cao minh tâm ghi là "2k 3" và "k 3" có nghĩa là gì
Đúng 0
Bình luận (0)
Cho ba vecto
a
→
,
b
→
,
c
→
trong không gian. Chứng minh rằng nếu
m
a
→
+
n
b
→
+
p
c
→
0...
Đọc tiếp
Cho ba vecto a → , b → , c → trong không gian. Chứng minh rằng nếu m a → + n b → + p c → = 0 → và một trong ba số m, n, p khác không thì ba vecto a → , b → , c → đồng phẳng
Giả sử p ≠ 0 ta có:
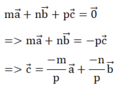
Do đó, ba vecto a → , b → , c → đồng phẳng theo định lí 1
Đúng 0
Bình luận (0)
chứng minh rằng nếu ba số a , b ,c lập thành một cấp số cộng thì : a2+8bc=(2b+c)2
Chứng minh rằng nếu a, b, c là ba số thỏa mãn a + b +c = 2013 và 1/a + 1/b + 1/c = 1/2013 thì phải có một trong ba số bằng 2013
chứng minh rằng nếu a+b+c=2021 và 1/a+1/b+1/c=2021 thì 1 trong ba số đó băng 2021
1/2021 thì giải được
Từ đề bài ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\Leftrightarrow\frac{ab+bc+ca}{abc}=\frac{1}{a+b+c}\)
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
Vậy một trong 3 số a+b,b+c,c+a bằng 0 hay ta có đpcm
Chứng minh rằng nếu ba số lập thành một cấp số nhân, đồng thời lập thành cấp số cộng thì ba số ấy bằng nhau.
Gọi 3 số đó là a - d, a, a + d rồi áp dụng tính chất của cấp số cộng và cấp số nhân.
Đúng 0
Bình luận (0)
chứng minh rằng: nếu ba số a, b, c là 3 số hạng liên tiếp của một cấp số cộng thì b bằng trung bình cộng của a và c
Chứng minh rằng: Nếu tam giác ABC có góc A tù và độ dài ba cạnh là ba số tự nhiên liên tiếp thì độ dài các cạnh đó bằng 2,3,4











