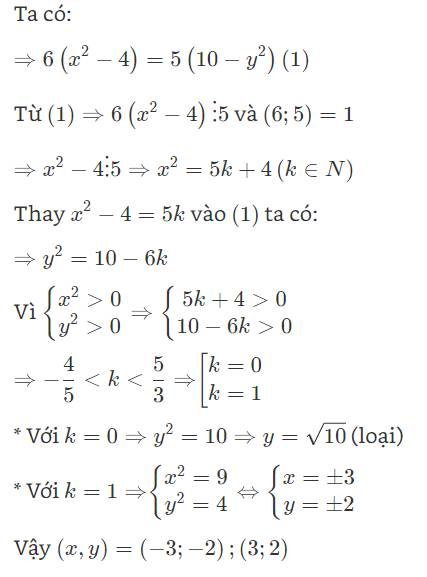6x^2 - 5y^2 = 74

<=> 6(x^2 - 4) = 5(10 - y^2)

--> 6(x^2 - 4) chia hết cho 5. Mà ƯCLN(6; 5) = 1

--> x^2 - 4 chia hết cho 5

Đặt x^2 = 5k + 4 (k tự nhiên)

--> y^2 = 10 - 6k

Do x^2, y^2 > 0 nên 5k + 4, 10 - 6k > 0 --> -4/5 < k < 5/3

--> k = 0 hoặc k = 1

TH1: k = 0 --> y = sqrt(10) (loại)

TH2: k = 1

--> (x; y) = (-3; -2); (3; 2) (thỏa)

6x^2 +5y^2 =74

(1) 6x2≥0 ⇒ 5y2≤74 ⇔

 y2≤745<15 ⇔ y2≤14

⇒y ={±3;±2;±1;0} 6x2≥0 ⇒5y2 ≤74⇔ y2≤745<15⇔ y2≤14 ⇒y={±3;±2;±1;0}

(2)x;y thuộc Z => 6x^2 luôn là số chẵn => y phải chẵn

(3) 6x^2 luôn chia hết cho 3 (74=7+4=11) không chia hết cho 3

=> y không chia hết cho 3

từ (1) (2) và (3) => y=±2y=±2

⇔6x2=74−5.4=54⇔x2=9;x=±3⇔6x2=74−5.4=54⇔x2=9;x=±3

(x;y)=(±3;±2)

6x^2 - 5y^2 = 74

<=> 6(x^2 - 4) = 5(10 - y^2)

--> 6(x^2 - 4) chia hết cho 5. Mà ƯCLN(6; 5) = 1

--> x^2 - 4 chia hết cho 5

Đặt x^2 = 5k + 4 (k tự nhiên)

--> y^2 = 10 - 6k

Do x^2, y^2 > 0 nên 5k + 4, 10 - 6k > 0 --> -4/5 < k < 5/3

--> k = 0 hoặc k = 1

TH1: k = 0 --> y = sqrt(10) (loại)

TH2: k = 1

--> (x; y) = (-3; -2); (3; 2) (thỏa)

vì 6x² và 74 \(⋮2\)

=> 5y² \(⋮2\)

=> y² \(⋮2\)( vì (5,2) = 1 )

=> y = 2 ( vì 2 là số nguyên tố chẵn duy nhất )

thay y = 2 vào bài ta được:

6x² + 5.4 = 74

6x² = 54

x² = 9 

=> x = 3

vậy x = 3 và y = 2

 6x² + 5y² = 74 (1) 
Ta có : 5x² + 5y² =< 6x² + 5y² =< 6x² + 6y²
<=> 5(x² + y²) =< 74 =< 6(x² + y²) 
<=> 12,3 =< x² + y² =< 14,8 
<=> 13 =< x² + y² =< 14 (vì x, y tự nhiên => x² + y² tự nhiên) 
Trường hợp 1 : x² + y² = 13 (2) 
Ta có hệ : 
6x² + 5y² = 74 (1) 
x² + y² = 13 (2) 
<=> 6x² + 5y² = 74 
5x² + 5y² = 65 
Trừ 2 phương trình : x² = 9 <=> x = 3 (vì x >= 0) 
Thay vào (2) y² = 13 - x² = 13 - 9 = 4 <=> x = 2 
Nghiệm : (x ; y) = (2 ; 3) 
Trường hợp 2 : x² + y² = 14 (4) 
Ta có hệ : 
6x² + 5y² = 74 (1) 
x² + y² = 14 (3) 
<=> 6x² + 5y² = 74 
5x² + 5y² = 70 
Trừ 2 phương trình : x² = 4 <=> x = 2 
Thay vào (3) : y² = 14 - 4 = 10 <=> y = \(\sqrt{10}\) (loại) 
Vậy phương trình có nghiệm nguyên duy nhất là (x ; y) = (2 ; 3) .

6x^2 +5y^2 =74

(1) 6x2≥0 ⇒ 5y2≤74 ⇔

 y2≤745<15 ⇔ y2≤14

⇒y ={±3;±2;±1;0} 6x2≥0 ⇒5y2 ≤74⇔ y2≤745<15⇔ y2≤14 ⇒y={±3;±2;±1;0}

(2)x;y thuộc Z => 6x^2 luôn là số chẵn => y phải chẵn

(3) 6x^2 luôn chia hết cho 3 (74=7+4=11) không chia hết cho 3

=> y không chia hết cho 3

từ (1) (2) và (3) => y=±2y=±2

⇔6x2=74−5.4=54⇔x2=9;x=±3⇔6x2=74−5.4=54⇔x2=9;x=±3

(x;y)=(±3;±2)

Ta có:

\(6x^2+5y^2=74\left(1\right)\)

Từ \(\left(1\right)\Rightarrow\hept{\begin{cases}x^2+1⋮5\\0< x^2\le12\end{cases}\Rightarrow\orbr{\begin{cases}x^2=4\\x^2=9\end{cases}}}\)

Với \(x^2=4\Rightarrow y^2=10\) (loại)

Với \(x^2=9\Rightarrow y^2=4\) (thỏa mãn)

\(\Rightarrow\hept{\begin{cases}x^2=9\\y^2=4\end{cases}\Rightarrow\hept{\begin{cases}x=\sqrt{9}\\y=\sqrt{4}\end{cases}\Rightarrow}\hept{\begin{cases}x=\left(-3;3\right)\\y=\left(-2;2\right)\end{cases}}}\)

Vậy...

Sai bét  nha bạn của tui

y² lớn hơn hoặc bằng 0

=> 5y² lớn hơn hoặc bằng 0

=> 6y² bé hơn hoặc bằng 74

=>x²<74/6<13

vì x nguyên => x² nhận các giá trị : 0;1;4;9

Rồi ghi ra từng th là xong

Trà Chanh gkm bây

Ta có : \(6x^2+5y^2=74\)

\(\Leftrightarrow\left(x^2+1\right)+5\left(x^2+y^2\right)=75\)

Ta thấy : \(\hept{\begin{cases}5\left(x^2+y^2\right)⋮5\\75⋮5\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}x^2+1⋮5\\0\le x^2\le12\end{cases}}\)  \(\Rightarrow\orbr{\begin{cases}x^2=4\\x^2=9\end{cases}}\)

* Nếu : \(x^2=4\Rightarrow\orbr{\begin{cases}x=2\\x=-2\end{cases}}\)

....

Bạn làm tiếp, thay các biến x vào biểu thức bản đầu để tìm ra y.

 6x2
 + 5y2
 = 74 (1) 
Ta có : 5x2
 + 5y2
 =< 6x2
 + 5y2
 =< 6x2
 + 6y2
<=> 5(x2
 + y2
) =< 74 =< 6(x2
 + y2
) 
<=> 12,3 =< x2
 + y2
 =< 14,8 
<=> 13 =< x2
 + y2
 =< 14 (vì x, y tự nhiên => x2
 + y2
 tự nhiên) 
Trường hợp 1 : x2
 + y2
 = 13 (2) 
Ta có hệ : 
6x2
 + 5y2
 = 74 (1) 
x
2
 + y2
 = 13 (2) 
<=> 6x2
 + 5y2
 = 74 
5x2
 + 5y2
 = 65 
Trừ 2 phương trình : x2
 = 9 <=> x = 3 (vì x >= 0) 
Thay vào (2) y2
 = 13 - x2
 = 13 - 9 = 4 <=> x = 2 
Nghiệm : (x ; y) = (2 ; 3) 
Trường hợp 2 : x2
 + y2
 = 14 (4) 
Ta có hệ : 
6x2
 + 5y2
 = 74 (1) 
x
2
 + y2
 = 14 (3) 
<=> 6x2
 + 5y2
 = 74 
5x2
 + 5y2
 = 70 
Trừ 2 phương trình : x2
 = 4 <=> x = 2 
Thay vào (3) : y2
 = 14 - 4 = 10 <=> y = 10 (loại) 
Vậy phương trình có nghiệm nguyên duy nhất là (x ; y) = (2 ; 3)

 6x2
 + 5y2
 = 74 (1) 
Ta có : 5x2
 + 5y2
 =< 6x2
 + 5y2
 =< 6x2
 + 6y2
<=> 5(x2
 + y2
) =< 74 =< 6(x2
 + y2
) 
<=> 12,3 =< x2
 + y2
 =< 14,8 
<=> 13 =< x2
 + y2
 =< 14 (vì x, y tự nhiên => x2
 + y2
 tự nhiên) 
Trường hợp 1 : x2
 + y2
 = 13 (2) 
Ta có hệ : 
6x2
 + 5y2
 = 74 (1) 
x
2
 + y2
 = 13 (2) 
<=> 6x2
 + 5y2
 = 74 
5x2
 + 5y2
 = 65 
Trừ 2 phương trình : x2
 = 9 <=> x = 3 (vì x >= 0) 
Thay vào (2) y2
 = 13 - x2
 = 13 - 9 = 4 <=> x = 2 
Nghiệm : (x ; y) = (2 ; 3) 
Trường hợp 2 : x2
 + y2
 = 14 (4) 
Ta có hệ : 
6x2
 + 5y2
 = 74 (1) 
x
2
 + y2
 = 14 (3) 
<=> 6x2
 + 5y2
 = 74 
5x2
 + 5y2
 = 70 
Trừ 2 phương trình : x2
 = 4 <=> x = 2 
Thay vào (3) : y2
 = 14 - 4 = 10 <=> y = 10 (loại) 
Vậy phương trình có nghiệm nguyên duy nhất là (x ; y) = (2 ; 3)

Tham khảo nha !!! 

6x^2 +5y^2 =74

(1) 6x2≥0 ⇒ 5y2≤74 ⇔

 y2≤745<15 ⇔ y2≤14

⇒y ={±3;±2;±1;0} 6x2≥0 ⇒5y2 ≤74⇔ y2≤745<15⇔ y2≤14 ⇒y={±3;±2;±1;0}

(2)x;y thuộc Z => 6x^2 luôn là số chẵn => y phải chẵn

(3) 6x^2 luôn chia hết cho 3 (74=7+4=11) không chia hết cho 3

=> y không chia hết cho 3

từ (1) (2) và (3) => y=±2y=±2

⇔6x2=74−5.4=54⇔x2=9;x=±3⇔6x2=74−5.4=54⇔x2=9;x=±3

(x;y)=(±3;±2)