Một bài kiểm tra Toán lớp 1 xoay quanh câu 1D với đề bài yêu cầu: Tìm số lớn hơn 60 và nhỏ hơn 80 (60 < ... < 80) có 3 đáp án được đưa ra lần lượt là A. 61, B. 70 và C. 80.

Những câu hỏi liên quan
Một bài kiểm tra Toán lớp 1 xoay quanh câu 1D với đề bài yêu cầu: Tìm số lớn hơn 60 và nhỏ hơn 80 (60 ... 80) có 3 đáp án được đưa ra lần lượt là A. 61, B. 70 và C. 80.Vậy đáp án nào đúng?A. 61B. 70C. 81AI NHANH NHẤT NÀO?!ĐỐ VUI THUI NHÉ,KO PHẢI BÀI CỦA MK ĐÂU
Đọc tiếp
Một bài kiểm tra Toán lớp 1 xoay quanh câu 1D với đề bài yêu cầu: Tìm số lớn hơn 60 và nhỏ hơn 80 (60 < ... < 80) có 3 đáp án được đưa ra lần lượt là A. 61, B. 70 và C. 80.
 |
Vậy đáp án nào đúng?
A. 61
B. 70
C. 81
AI NHANH NHẤT NÀO?!
ĐỐ VUI THUI NHÉ,KO PHẢI BÀI CỦA MK ĐÂU
cả A và B đều đúng mà chỉ đc khoanh có 1 câu thôi thì khoanh vào 61 cx đúng mà sao lại bảo sai ai ra đề này thì chắc ko bình thường
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Người ra đề yêu cầu chọn từ dãy số 1, 3, 5, 7, 9, 11, 13, 15 ra ba số để điền vào ô trống sao cho tổng kết quả ba ô là 30. Các số có thể được sử dụng nhiều hơn một lần.Người giới thiệu bài toán khẳng định chỉ khoảng 2% người tham gia có thể giải bài này. Phần lớn người giải cho rằng bài toán không có đáp án vì tổng 3 số lẻ luôn là số lẻ.Tuy nhiên, đáp án chắc chắn sẽ khiến nhiều người bất ngờ.Liệu bạn có nằm trong số 2% người có thể đưa ra đáp số cho bài toán tưởng chừng không có lời giải này?
Đọc tiếp
Người ra đề yêu cầu chọn từ dãy số 1, 3, 5, 7, 9, 11, 13, 15 ra ba số để điền vào ô trống sao cho tổng kết quả ba ô là 30. Các số có thể được sử dụng nhiều hơn một lần.
Người giới thiệu bài toán khẳng định chỉ khoảng 2% người tham gia có thể giải bài này. Phần lớn người giải cho rằng bài toán không có đáp án vì tổng 3 số lẻ luôn là số lẻ.
Tuy nhiên, đáp án chắc chắn sẽ khiến nhiều người bất ngờ.
Liệu bạn có nằm trong số 2% người có thể đưa ra đáp số cho bài toán tưởng chừng không có lời giải này?
5,5+9,5+15=30 hay 7,5+9,5+13=30.
15+(15)= 30.
Đúng 0
Bình luận (0)
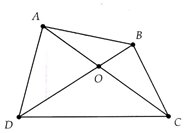
Bài 1: Cho tứ giác ABCD. Chứng minh:
a) Tổng hai cạnh đối nhỏ hơn tổng hai đường chéo
b) Tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
Bài 2: Cho tứ giác ABCD có góc A70 độ , góc D80 độ và góc ngoài ở đỉnh C60 độ
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối của tứ giác đó.
Bài 3: Tứ giác ABCD có góc C + góc D 90 độ. Chứng minh rằng AC2+ BD2 AB2+ CD2
Mình đang rất cần các bài này. Các bạn giúp mình nhé. cả...
Đọc tiếp
Bài 1: Cho tứ giác ABCD. Chứng minh:
a) Tổng hai cạnh đối nhỏ hơn tổng hai đường chéo
b) Tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
Bài 2: Cho tứ giác ABCD có góc A=70 độ , góc D=80 độ và góc ngoài ở đỉnh C=60 độ
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối của tứ giác đó.
Bài 3: Tứ giác ABCD có góc C + góc D= 90 độ. Chứng minh rằng AC2+ BD2= AB2+ CD2
Mình đang rất cần các bài này. Các bạn giúp mình nhé. cảm ơn các bạn
Bài 1: 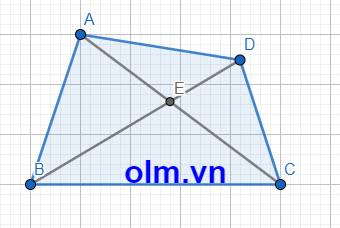
Gọi E là giao điểm của hai đường chéo AC và BD
Xét tam giác AEB ta có: AE + BE > AB (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét tam giác DEC ta có: DE + CE > DC (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AE + BE + DE + CE > AB + DC
(AE + CE) + (BE + DE) > AB + DC
AC + BD > AB + DC
Tương tự ta có AC + BD > AD + BC
Kết luận: Trong một tứ giác tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối.
Nửa chu vi của tứ giác ABCD là: \(\dfrac{AB+BC+CD+DA}{2}\)
Theo chứng minh trên ta có:
\(\dfrac{AB+BC+CD+DA}{2}\)< \(\dfrac{\left(AB+CD\right)\times2}{2}\) = AB + CD (1)
Vì trong một tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại nên ta có:
AB + AD > BD
AB + BC > AC
BC + CD > BD
CD + AD > AC
Cộng vế với vế ta có:
(AB + BC + CD + DA)\(\times\)2 > (BD + AC ) \(\times\) 2
⇒AB + BC + CD + DA > BD + AC (2)
Kết hợp (1) và (2) ta có:
Tổng hai đường chéo của tứ giác lớn hơn nửa chu vi của tứ giác nhưng nhỏ hơn chu vi của tứ giác
Đúng 0
Bình luận (0)
Bài : 2 Góc C = 1800 - 600 = 1200
Tổng bốn góc của tứ giác là 3600
Ta có: Góc B của tứ giác ABCD là:
3600 - (700 + 800 + 1200) = 900
Câu b chứng minh như bài 1
Đúng 0
Bình luận (0)
Bài 1:
a) Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC,OCD và ODA.
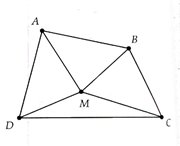
b) Chứng minh tổng hai đường chéo lớn hơn nửa chu vi tứ giác sử dụng kết quả của a).
Chứng minh tổng hai đường chéo nhỏ hơn chu vi tứ giác sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác ABC, ADC, ABD và CBD
Bài 3:
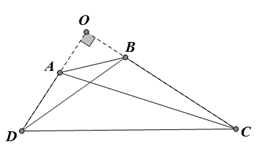
Gọi O là giao điểm AD và BC.
Ta có nên
Áp dụng định lí Py – ta – go,
Ta có
Nên
Đúng 0
Bình luận (0)
Bài 1: Cho tứ giác ABCD. Chứng minh:
a) Tổng hai cạnh đối nhỏ hơn tổng hai đường chéo
b) Tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
Bài 2: Cho tứ giác ABCD có góc A70 độ , góc D80 độ và góc ngoài ở đỉnh C60 độ
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối của tứ giác đó.
Bài 3: Tứ giác ABCD có góc C + góc D 90 độ. Chứng minh rằng AC2+ BD2 AB2+ CD2
Mình đang rất cần các bài này. Các bạn giúp mình nhé. cả...
Đọc tiếp
Bài 1: Cho tứ giác ABCD. Chứng minh:
a) Tổng hai cạnh đối nhỏ hơn tổng hai đường chéo
b) Tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
Bài 2: Cho tứ giác ABCD có góc A=70 độ , góc D=80 độ và góc ngoài ở đỉnh C=60 độ
a) Tính góc B của tứ giác ABCD
b) Chứng minh rằng tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối của tứ giác đó.
Bài 3: Tứ giác ABCD có góc C + góc D= 90 độ. Chứng minh rằng AC2+ BD2= AB2+ CD2
Mình đang rất cần các bài này. Các bạn giúp mình nhé. cảm ơn các bạn
Câu 6: Cho tam giác ABC có: AB 2cm; BC 4cm; AC 5cm. Thì:A. góc A lớn hơn góc B B.góc B lớn hơn góc CC.góc A nhỏ hơn góc CD.góc B nhỏ hơn góc CCâu 7: Cho tam giác ABC có ba góc A, B, C có số đo lần lượt là: 80 0 , 40 0 , 60 0 . Thì:A.AB BCB.AB ACC.BC ACD.Đáp án B và C đúngCâu 08:Cho tam giác ABC và tam giác DEF có abed,bcef. Thêm điều kiện nào sau đây để tam giác ABC tam giác DEF? A. góc A góc D B. góc C góc F C.AB ACD.AC DF
Đọc tiếp
Câu 6: Cho tam giác ABC có: AB = 2cm; BC = 4cm; AC = 5cm. Thì:
A. góc A lớn hơn góc B
B.góc B lớn hơn góc C
C.góc A nhỏ hơn góc C
D.góc B nhỏ hơn góc C
Câu 7: Cho tam giác ABC có ba góc A, B, C có số đo lần lượt là: 80 0 , 40 0 , 60 0 . Thì:
A.AB > BC
B.AB > AC
C.BC > AC
D.Đáp án B và C đúng
Câu 08:
Cho tam giác ABC và tam giác DEF có ab=ed,bc=ef. Thêm điều kiện nào sau đây để tam giác ABC = tam giác DEF?
A. góc A = góc D
B. góc C = góc F
C.AB = AC
D.AC = DF
Xem thêm câu trả lời
Bài 9: Cho tam giác DEF có D^ - F^ 50° và E^ 80°. Số đo của góc D^ và F^ lần lượt là?Bài 10: Cho hình sau. Tính số đo góc x.A. 40°B. 50°C. 60°D. 70°
Đọc tiếp
Bài 9: Cho tam giác DEF có D^ - F^ = 50° và E^ = 80°. Số đo của góc D^ và F^ lần lượt là?
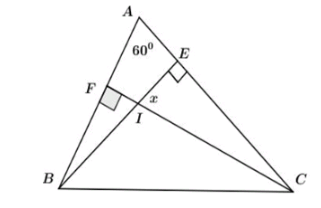
Bài 10: Cho hình sau. Tính số đo góc x.
A. 40°
B. 50°
C. 60°
D. 70°
Câu 1 lỗi font còn câu 2 là 60 độ nhé do x và góc A đều bù góc FIE
Đúng 1
Bình luận (3)
Bạn nào hãy giúp mình với mình có một câu chuyện như sau:Lớp nọ có một thằng lớp trưởng tên... Nó nổi tiếng là ăn gian điểm.Lần 1: đó là kiểm tra 15 phút Công nghệ, nó được 8.8 điểm hay thấp hơn 8.8 mà nó hô để cô vào sổ là 9.0 đLần 2: Kiểm tra miệng môn Anh văn (lớp đó kiểm tra miệng môn anh văn bằng giấy) nó được 8 điểm mà hô lên 9 điểm thằng này ăn gian quá mứcLần 3: Kiểm tra 15 phút Anh văn nó được bao nhiêu điểm không biết mà nó tự nó phát bài cho các bạn rồi lật đật giấu luôn đề nó lúc đầu...
Đọc tiếp
Bạn nào hãy giúp mình với mình có một câu chuyện như sau:
Lớp nọ có một thằng lớp trưởng tên... Nó nổi tiếng là ăn gian điểm.
Lần 1: đó là kiểm tra 15 phút Công nghệ, nó được 8.8 điểm hay thấp hơn 8.8 mà nó hô để cô vào sổ là 9.0 đ
Lần 2: Kiểm tra miệng môn Anh văn (lớp đó kiểm tra miệng môn anh văn bằng giấy) nó được 8 điểm mà hô lên 9 điểm thằng này ăn gian quá mức
Lần 3: Kiểm tra 15 phút Anh văn nó được bao nhiêu điểm không biết mà nó tự nó phát bài cho các bạn rồi lật đật giấu luôn đề nó lúc đầu nó nói 7.5 đ mà hô lên là 7.8 mà chưa chắc gì nó được 7.5 đ nữa. Nó học dốt lắm toàn quay cóp bài của 2 bạn ở trên nó nhất là bạn HSG Toán nhất là vào khi kiểm tra Toán.
Lần 4: mà mới hồi hôm qua đây thầy Toán phát đề Toán 1 tiết số nó lật đật giấu nữa rồi nó hô là 7.5 điểm mà thằng đó dốt lắm chắc gì đã được 5 điểm đâu mà.
Bạn hãy tìm ra cách giải quyết chuyện trên và tìm ra tên của nó.
Bình luận nhiều vào khi đã bí hết mk sẽ cho ra đáp án.
Chuyện của nó thì kệ , chẳng liên quan đến mình. Nó như vậy thì mình hay ng khc cx chẳng bị lm sao nên chẳng phải xử lí cái gì. Mà đã thấy ức chế sao không nói luôn lúc nó nói dối đi đợi đến bây giờ đăng lên diễn đàn.
Kết luận: Câu chuyện quá dở , câu từ cũng không hay, không có kết thúc hay phần gay cấn, nếu đặt tên thì theo mink là: Thằng học ngu.
Đúng 0
Bình luận (0)
Câu a: Một vật dao động với tần số 8Hz. Hỏi trong một phút vật thực hiện được bao nhiêu dao động?A. 7,5 dao độngB. 8 dao độngC. 480 dao độngD. 60 dao độngCâu b: Có 4 con lắc đơn có chiều dài lần lượt là 50 cm, 60 cm, 70 cm và 80 cm. Con lắc có tần số dao động lớn nhất là con lắc có chiều dài:A. 50 cm B. 60 cmC. 70 cm D. 80 cm
Đọc tiếp
Câu a: Một vật dao động với tần số 8Hz. Hỏi trong một phút vật thực hiện được bao nhiêu dao động?
A. 7,5 dao động
B. 8 dao động
C. 480 dao động
D. 60 dao động
Câu b: Có 4 con lắc đơn có chiều dài lần lượt là 50 cm, 60 cm, 70 cm và 80 cm. Con lắc có tần số dao động lớn nhất là con lắc có chiều dài:
A. 50 cm B. 60 cm
C. 70 cm D. 80 cm
Tôi là giáo viên gia sư Toán cấp 1-2-3. Tôi có học trò lớp 6 hỏi bài toán như sau: Tìm số tự nhiên nhỏ hơn 500, biết rằng khi chia 8, 10, 15, 20 có số dư theo thứ tự là 5, 7, 12, 17 và chia hết cho 51.Tôi đã giải như sau:Gọi a là số tự nhiên cần tìm, thương a chia cho 8, 10, 15, 20 lần lượt là b, c, d, e.Ta có đẳng thức: a 8b + 5 10c + 7 15d + 12 20e + 17Suy ra B(8) – 5 B(10) – 7 B(15) – 12 B(20) – 17Suy ra B(10) – B(8) 2; B(15) – B(10) 5; B(20) – B(15) 5.B(8) {0; 8; 16; 30; 40;48; 56...
Đọc tiếp
Tôi là giáo viên gia sư Toán cấp 1-2-3. Tôi có học trò lớp 6 hỏi bài toán như sau: Tìm số tự nhiên nhỏ hơn 500, biết rằng khi chia 8, 10, 15, 20 có số dư theo thứ tự là 5, 7, 12, 17 và chia hết cho 51.
Tôi đã giải như sau:
Gọi a là số tự nhiên cần tìm, thương a chia cho 8, 10, 15, 20 lần lượt là b, c, d, e.
Ta có đẳng thức: a = 8b + 5 = 10c + 7 = 15d + 12 = 20e + 17
Suy ra B(8) – 5 = B(10) – 7 = B(15) – 12 = B(20) – 17
Suy ra B(10) – B(8) = 2; B(15) – B(10) = 5; B(20) – B(15) = 5.
B(8) = {0; 8; 16; 30; 40;48; 56; 64; 72; 80; 88; 96; 104; 112; 120…}
B(10) = {0; 10; 20; 30; 40; 50; 60; 70; 80; 90; 100; 110; 120; 130; 140; 150; 160;…}
B(15) = {0; 15; 30; 45; 60; 75; 90; 105; 120; 135; 150; 165; …}
B(20) = {0; 20; 40; 60; 80; 100; 120; 140; 160; 180; 200; 220; 240; 260;…}
Để có B(10) – B(8) = 2 ta tìm được cặp 10 – 8; 90 – 88, …
Để có B(15) – B(10) = 5 ta tìm được cặp 15 – 10; 105 – 100, …
Để có B(20) – B(15) = 5 ta tìm được cặp 20 – 15; 80 – 75; 140-135, …
Tuy nhiên để cùng thỏa mãn B(8) – 5 = B(10) – 7 = B(15) – 12 = B(20) – 17 thì ta chọn ở B(8) số 8, ở B(10) số 10, ở B(15) số 15, ở B(20) số 20. Điều này có nghĩa là
8 – 5 = 10 – 7 = 15 – 12 = 20 – 17 = 3.
Con số 3 này gợi ý cho ta cộng thêm vào đẳng thức: a = 8b + 5 = 10c + 7 = 15d + 12 = 20e + 17 hai vế với 3 ta có: a + 3 = 8b + 5 + 3 = 10c + 7 + 3 = 15d + 12 + 3 = 20e + 17 + 3
Suy ra: a + 3 = 8(b + 1) = 10(c + 1) = 15(d + 1) = 20(e + 1)
Suy ra a + 3 chia hết cho 8, 10, 15, 20.
BCNN(8, 10, 15, 20) = 23.3.5 = 120
Suy ra a + 3 thuộc BC(120) = {0; 120; 240; 360; 480; 600; 720;… }
Suy ra a thuộc {-3; 117; 237; 357; 477; 597; 717;…}
Để a nhỏ hơn 500 suy ra a thuộc {-3; 117; 237; 357; 477}
Để a chia hết cho 51 thì chỉ có a = 357 là thỏa mãn.
Vậy số tự nhiên a nhỏ hơn 500 thỏa mãn điều kiện của bài toán là 357.
Ui thầy giỏi ghê ha! Thán phục! Thán phục????????
Đúng 0
Bình luận (0)