Cho tam giác ABC,ta có các bất đẳng thức
AB+BC lớn hơn AC
Đề bài: Cho điểm M nằm trong tam giác ABC. CM: Tổng MA+MB+MC lớn hơn nửa chu vi và bé hơn chu vi của tam giác đó.
Mình giải cách sau có đúng ko?
--Ta có: MB+MA>AB (Bất đẳng thức tam giác)
MC+MB>BC (Bất đẳng thức tam giác)
MA+MC>AC (Bất đẳng thức tam giác)
=> MB+MA+MC+MB+MA+MC>AB+BC+AC
=> 2MA+2MB+2MC > 2P
=> MA+MB+MC > P (được phần CM)
--Ta có: MA+AB>MB (Bất đẳng thức tam giác)
MB+BC>MC (Bất đẳng thức tam giác)
MC+AC>MA (Bất đẳng thức tam giác)
=> MA+AB+MB+BC+MC+AC>MB+MC+MA
=> MA+MB+MC+2P > MB+MC+MA
=> 2P >MA+MB+MC (được phần CM)
Mong các bạn có thể trả lời sớm nhất.
Đề bài: Cho điểm M nằm trong tam giác ABC. CM: Tổng MA+MB+MC lớn hơn nửa chu vi và bé hơn chu vi của tam giác đó.
Mình giải cách sau có đúng ko?
--Ta có: MB+MA>AB (Bất đẳng thức tam giác)
MC+MB>BC (Bất đẳng thức tam giác)
MA+MC>AC (Bất đẳng thức tam giác)
=> MB+MA+MC+MB+MA+MC>AB+BC+AC
=> 2MA+2MB+2MC > 2P
=> MA+MB+MC > P (được phần CM)
--Ta có: MA+AB>MB (Bất đẳng thức tam giác)
MB+BC>MC (Bất đẳng thức tam giác)
MC+AC>MA (Bất đẳng thức tam giác)
=> MA+AB+MB+BC+MC+AC>MB+MC+MA
=> MA+MB+MC+2P > MB+MC+MA
=> 2P >MA+MB+MC (được phần CM)
Mong các bạn có thể trả lời sớm nhất.
Một cách chứng minh khác của bất đẳng thức:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường thẳng vuông góc AH đến đường thẳng BC.
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông để chứng minh AB+ AC> BC.
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại.
a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. kẻ đường vuông góc AH đến đường thẳng BC (H ε BC)
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông để chứng minh AB + AC > BC
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại
a) Xét tam giác vuông AHC có AC là cạnh lớn nhất ( cạnh lớn nhất trong tam giác vuông) => AC>HC (1) Xét tam giác vuông AHB có AB là cạnh lớn nhất (canh lớn nhất trong tam giác vuông) =>AB>HB (2) Ta có : HC+HB+BC ( H nằm giũa A và C) (3) Từ (1) , (2) và (3) => AC+AB>BC b)Xét tam giác ABC có BC là cạnh lớn nhất(gt) =>BC>AB Ta có : AC>0 => BC+AC>AB Xét tam giác ABC có BC là cạnh lớn nhất (gt) =>BC>AC Vì AB>0=>BC+AB>AC
Đề bài: Cho điểm M nằm trong tam giác ABC. CM: Tổng MA+MB+MC lớn hơn nửa chu vi và bé hơn chu vi của tam giác đó.
Mình giải cách sau có đúng ko?
--Ta có: MB+MA>AB (Bất đẳng thức tam giác)
MC+MB>BC (Bất đẳng thức tam giác)
MA+MC>AC (Bất đẳng thức tam giác)
=> MB+MA+MC+MB+MA+MC>AB+BC+AC
=> 2MA+2MB+2MC > 2P
=> MA+MB+MC > P (được phần CM)
--Ta có: MA+AB>MB (Bất đẳng thức tam giác)
MB+BC>MC (Bất đẳng thức tam giác)
MC+AC>MA (Bất đẳng thức tam giác)
=> MA+AB+MB+BC+MC+AC>MB+MC+MA
=> MA+MB+MC+2P > MB+MC+MA
=> 2P >MA+MB+MC (được phần CM)
Mong các bạn có thể trả lời sớm nhất.
bạn làm chính xác rùi
ôi thần linh ơi
bài này mình giải sai rùi,mai phải nộp cho thầy cám ơn nhé
ủng hộ nha mọi người
trên thế giới này tui ghét nhất cái câu ôi thần linh ơi, mỗi khi con phim ấn độ nhất là cô dâu 8 tuổi nghe cái câu đó tắt tv nghỉ coi luôn
ủa, mình tưởng AB+AC+BC=P thôi chứ sao lại bằng 2P???
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC (H thuộc BC).
Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở Bài 1 để chứng minh AB + AC > BC.
Theo giả thiết, tam giác ABC có độ dài cạnh BC là lớn nhất nên chân đường vuông góc kẻ từ A đến cạnh BC chắn chắn phải nằm giữa B và C.
Suy ra H nằm giữa B và C.
⇒ HB + HC = BC
+) Xét tam giác AHB vuông tại H ta có: HB < AB (1) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
+) Xét tam giác AHC vuông tại H ta có: HC < AC (2) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
Lấy (1) + (2) ta được:
HB + HC < AB + AC
Mà HB + HC = BC suy ra BC < AB + AC hay AB + AC > BC
Chứng minh “Bất đẳng thức tam giác mở rộng ”: Với ba điểm A, B, C bất kỳ, ta có AB + AC ≥ BC
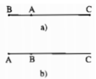
- Nếu A, B, C không thẳng hàng thì 3 điểm A, B, C tạo thành 3 đỉnh của 1 tam giác.
Trong tam giác ABC ta có AB + AC > BC
- Nếu A, B, C thẳng hàng và A ở giữa B và C hoặc trùng B, C thì AB + AC = BC
• Nếu A nằm giữa B và C thì AB + AC = BC.
• Nếu B nằm giữa A và C thì AB + BC = AC nên AC > BC.
Suy ra: AC + AB > BC
• Nếu C nằm giữa A và B thì AC + CB = AB nên AB > BC.
Suy ra: AB + AC > BC.
Vậy với ba điểm A, B, C bất kỳ ta luôn có AB + AC ≥ BC
Một cách chứng minh khác của bất đẳng thức tam giác :
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC \(\left(H\in BC\right)\)
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở bài 1 để chứng minh AB + AC > BC
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại
a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)
Cho tam giác ABC. Chứng minh bất đẳng thức sau:
a) AB + BC > AC.
b) AC + BC > AB.