tìm các sô nguyên x,y,z,,t thoả mãn: 1/10001=1234/x=y/45674567=2345/t

Những câu hỏi liên quan
tìm các sô nguyên x,y,z,,t thoả mãn: 1/10001=1234/x=y/45674567=2345/t
Answer:
\(\frac{1}{10001}=\frac{1234}{x}=\frac{y}{45674567}=\frac{2345}{t}\)
\(\Rightarrow\hept{\begin{cases}x=1234.10001=12341234\\y=45674567:10001=4567\\t=2345.10001=23452345\end{cases}}\)
sao ko ai trả lời zậy
tìm các cặp số nguyên x,y thoả mãn x^2+xy=2022x+2023y+2024 (cần gấp)
Tìm các số nguyên x thoả mãn: (x + 4) ⋮ (x + 1)
Ta có x + 4 = (x + 1) + 3
nên (x + 4) ⋮ (x + 1) khi 3 ⋮ (x + 1), tức là x + 1 là ước của 3.
Vì Ư(3) = {-1; 1; -3; 3} ta có bảng sau:

Đáp số x = -4; -2; 0; 2.
Đúng 0
Bình luận (0)
Tìm tất cả các cặp số nguyên dương x,y thoả mãn: \(4x^2\left(x+17x\right)-68xy+17y^2=161312\)
bài 1: tìm tất cả các cặp số nguyên (x,y) thoả mãn phương trình:
x^2-25=y.(y+6)
cac ban oi giup minh. minh dàng can gap
Cho x,y,z là các số thực dương thoả mãn x+y+z=3. Tìm giá trị nhỏ nhất của biểu thức \(P=x^4+2y^4+3z^4\) ( với 8 chữ số thập phân sau dấu phẩy)
Tìm các số nguyên x thoả mãn: (4x + 3) ⋮ (x - 2).
Ta có 4x + 3 = 4(x - 2) + 11
nên (4x + 3) ⋮ (x - 2) khi 11 ⋮ (x - 2), tức là x -2 là ước của 11
Ư(11) = { -11; -1; 1; 11}; ta có bảng sau:
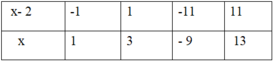
Vậy các số nguyên x thỏa mãn là: x ∈ { 1; 3; - 9; 13}
Đúng 0
Bình luận (0)
Tìm tất cả các số nguyên x thoả mãn: -10 < x < 15.
Các số nguyên x thỏa mãn -10 < x < 15 là:
x ∈ { -9; -8; -7; ...; -1; 0; 1; 2; ...; 13; 14}
Đúng 0
Bình luận (0)
Cho x, y, z thoả mãn \(\sqrt{x}+\sqrt{y}+\sqrt{z}=3\). Tìm giá trị nhỏ nhất của biểu thức \(P=\frac{\sqrt{x}+1}{y+1}+\frac{\sqrt{y}+1}{z+1}+\frac{\sqrt{z}+1}{x+1}\)
Lời giải:
\(P=(\sqrt{x}+1)-\frac{y(\sqrt{x}+1)}{y+1}+(\sqrt{y}+1)-\frac{z(\sqrt{y}+1)}{z+1}+(\sqrt{z}+1)-\frac{x(\sqrt{z}+1)}{x+1}\)
\(=(\sqrt{x}+\sqrt{y}+\sqrt{z}+3)-\left[\frac{y(\sqrt{x}+1)}{y+1}+\frac{z(\sqrt{y}+1)}{z+1}+\frac{x(\sqrt{z}+1)}{x+1}\right]\)
\(=6-\left[\frac{y(\sqrt{x}+1)}{y+1}+\frac{z(\sqrt{y}+1)}{z+1}+\frac{x(\sqrt{z}+1)}{x+1}\right](1)\)
Áp dụng BĐT Cauchy:
\(\frac{y(\sqrt{x}+1)}{y+1}+\frac{z(\sqrt{y}+1)}{z+1}+\frac{x(\sqrt{z}+1)}{x+1}\leq \frac{y(\sqrt{x}+1)}{2\sqrt{y}}+\frac{z(\sqrt{y}+1)}{2\sqrt{z}}+\frac{x(\sqrt{z}+1)}{2\sqrt{x}}=\frac{\sqrt{x}+\sqrt{y}+\sqrt{z}+(\sqrt{xy}+\sqrt{yz}+\sqrt{xz})}{2}\)
Theo hệ quả quen thuộc của BĐT Cauchy: \((\sqrt{xy}+\sqrt{yz}+\sqrt{xz})\leq \frac{1}{3}(\sqrt{x}+\sqrt{y}+\sqrt{z})^2\)
\(\Rightarrow \frac{y(\sqrt{x}+1)}{y+1}+\frac{z(\sqrt{y}+1)}{z+1}+\frac{x(\sqrt{z}+1)}{x+1}\leq \frac{(\sqrt{x}+\sqrt{y}+\sqrt{z})+\frac{1}{3}(\sqrt{x}+\sqrt{y}+\sqrt{z})^2}{2}=3(2)\)
Từ \((1);(2)\Rightarrow P\geq 6-3=3\)
Vậy \(P_{\min}=3\Leftrightarrow x=y=z=1\)
Đúng 0
Bình luận (0)











