cho hình thang ABCD , biết Saob = 4cm vuông ; Sdoc = 9cm vuông . Tính Sabcd
cho hình thang vuông ABCD có AB//CD ( góc A=90 độ), AB=4cm, AD=6cm, CD=9cm.
a, tam giác BAD đông dạng tam giác ADC
b, AC vuông góc BD
c, tính \(\dfrac{Saob}{Scod}\)
Lời giải:
a)
Xét tam giác $BAD$ và $ADC$ có:
$\widehat{BAD}=\widehat{ADC}=90^0$
$\frac{AB}{AD}=\frac{4}{6}=\frac{6}{9}=\frac{AD}{DC}$
$\Rightarrow \triangle BAD\sim \triangle ADC$ (c.g.c)
b) Cho $O$ là giao $AC$ và $BD$
Từ tam giác đồng dạng p.a suy ra:
$\widehat{ABD}=\widehat{DAC}$
$\Leftrightarrow \widehat{ABO}=\widehat{DAO}=90^0-\widehat{BAO}$
$\Rightarrow \widehat{ABO}+\widehat{BAO}=90^0$
$\Rightarrow \widehat{AOB}=90^0$
$\Rightarrow AC\perp BD$ (đpcm)
c)
Theo định lý Talet:
$\frac{OA}{OC}=\frac{OB}{OD}=\frac{AB}{CD}=\frac{4}{9}$
$\Rightarrow OA=\frac{4}{9}OC; OB=\frac{4}{9}OD$
\(\frac{S_{AOB}}{S_{COD}}=\frac{OA.OB}{OC.OD}=\frac{\frac{4}{9}OC.\frac{4}{9}OD}{OC.OD}=\frac{16}{81}\)
cho hình thang ABCD có đáy nhỏ AB=1/3CD .Hai đường chéo AC và BD cắt nhau ở O biết SAOB=4CM vuông.tính SABCD
Cho hình thang abcd SAOB = 9cm2, SBOC = 25cm2. Tính diện tích hình thang ABCD
Cho hình thang ABCD . Cắt BD tại O . Tính diện tích hình thang ABCD biết diện tích tam giác AOB =4cm vuông, diện tích tam giác AOD =9cm vuông
Cho hình thang cân ABCD (AB//CD) có AC vuông góc với BD tại O. Biết AB=4cm, CD=8cm. Tính diện tích hình thang ABCD.
Cho hình vẽ bên, biết tứ giác ABCD hình thang vuông. Độ dài AB = DH = 4cm ; DC = 12 cm. Tính số đo góc ABC của hình thang ABCD ?
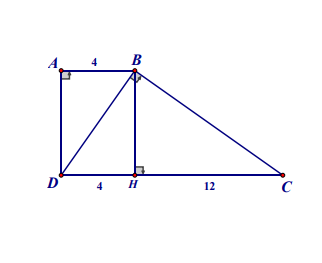
e cần gấp ạ
Áp dụng HTL:
\(BH^2=DH\cdot HC=48\Leftrightarrow BH=4\sqrt{3}\left(cm\right)\)
Dễ thấy ABHD là hcn nên \(BH=AD=4\sqrt{3}\left(cm\right)\)
Ta có:
\(\tan\widehat{ABD}=\dfrac{AD}{AB}=\dfrac{4\sqrt{3}}{4}=\sqrt{3}=\tan60^0\\ \Leftrightarrow\widehat{ABD}=60^0\\ \Leftrightarrow\widehat{ABC}=\widehat{ABD}+\widehat{CBD}=60^0+90^0=150^0\)
cho hình thang abcd biết 2 đường chéo cắt nhau tại o . biết Saob = 18 cm2 ,Saod =30 cm2 . tính Sabcd
Cho hình thang vuông ABCD vuông tại A và D. Biết AD = 3 cm và CD = 4cm. Tính AC?
A. 3cm
B. 4cm
C. 3,5cm
D. 5cm
Do tứ giác ABCD là hình thang vuông nên D ^ = 90 ° . Suy ra, tam giác ADC là tam giác vuông tại D.
Áp dụng định lí Pi-ta-go vào tam giác ACD vuông tại D ta có:
A C 2 = A D 2 + D C 2 = 3 2 + 4 2 = 25
Suy ra A C = 5 c m
Chọn đáp án D.
Cho hình thang ABCD cân ( AB//CD ) có DB là tia phân giác góc ,.BD vuông góc BC Biết AB=4cm Tính chu vi hình thang.
Cho hình thang ABCD, với chiều cao AH. Biết AD có 4cm, BH bằng 2cm, HC bằng 6cm và diện tích hình tam giác ABH là 6cm vuông. Tính diện tích hình thang ABCD?