cho tam giác ABC có góc B>C. kẻ đường cao AH và đường phân giác AD. CMR: AD nằm giữa AH và AC

Những câu hỏi liên quan
Cho tam giác ABC có góc B>góc C. Đường trung tuyến AM, đường phân giác AD, đường cao AH. Chứng minh: AD nằm giữa AH và AM
Gọi AD và AH lần lượt là đường phân giác và đường cao của tam giác ABC (H nằm giữa D và C). Các điểm M,N là chân các đường vuông góc của D tương ứng trên các cạnh AC, ABa, CMR dfrac{MC}{NB} dfrac{CH}{BH}b, BM cắt AH tại K. CMR dfrac{CK}{KH}dfrac{AM}{MC}.dfrac{CB}{BH}c, CMR CN đi qua K
Đọc tiếp
Gọi AD và AH lần lượt là đường phân giác và đường cao của tam giác ABC (H nằm giữa D và C). Các điểm M,N là chân các đường vuông góc của D tương ứng trên các cạnh AC, AB
a, CMR \(\dfrac{MC}{NB}\) =\(\dfrac{CH}{BH}\)
b, BM cắt AH tại K. CMR \(\dfrac{CK}{KH}\)=\(\dfrac{AM}{MC}\).\(\dfrac{CB}{BH}\)
c, CMR CN đi qua K
Cho tam giác ABC vuông tại A, kẻ đường cao AH và trung tuyến AM. đường phân giác góc A, cắt đường trung trực BC tại D. Từ D kẻ DE vuông góc với BA và DF vuông góc với AC.
a, CMR: AD là phân giác góc HAM
b, 3 điểm E, M, F thẳng hàng
c, Tam giác ABC là tam giác vuông cân
Cho tam giác ABC vuông tại A, kẻ đường cao AH và trung tuyến AM. đường phân giác góc A, cắt đường trung trực BC tại D. Từ D kẻ DE vuông góc với BA và DF vuông góc với AC.
a, CMR: AD là phân giác góc HAM
b, 3 điểm E, M, F thẳng hàng
c, Tam giác ABC là tam giác vuông cân
cho tam giác abc vuông tại a đường cao ah kẻ đường phân giác ad của tam giác CHA và đường phân giác bk của tam giác ABC(d thuoc bc ;k thuộc ac) bk cắt lần lượt ah và ad tại e và f cmr a, tam giác AHB đồng dạng với tam giác CHA b, tam gic AEF đồng dạng với tam giác BEH c, KD//AH d, eh/ab=kd/bc
Cho tam giác ABC vuông tại A, đường cao AH, tia phân giác góc HAC cắt BC tại D.
a. CMR tam giác ABD cân
b. Từ B kẻ đường thẳng vuông góc với AD cắt AC tại M. Chứng minh rằng MD//AH
c. Gọi E là giao điểm của AH và MB. CMR MD=AE
dễ quá k làm nx
Tam giác ABC có góc A = 90 0 , AB = 12cm, AC=16cm; đường phân giác góc A cắt BC tại D. Kẻ đường cao AH, tính AH, HD và AD.
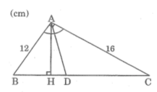
Ta có: S A B C = 1/2.AB.AC = 1/2.AH.BC
Suy ra: AB.AC = AH.BC
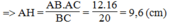
Trong tam giác vuông AHB, ta có: ∠ A H B = 90 0
Theo định lí Pi-ta-go, ta có: A B 2 = A H 2 + H B 2
Suy ra: H B 2 = A B 2 - A H 2 = 12 2 - 9 , 6 2 = 51,84 ⇒ HB =7,2 (cm)
Vậy HD = BD – HB = 60/7 - 7,2 ≈ 1,37 (cm)
Trong tam giác vuông AHD, ta có: ∠ A H D = 90 0
Theo định lí Pi-ta-go, ta có:
A D 2 = A H 2 + H D 2 = 9 , 6 2 + 1 , 37 2 = 94,0369
Suy ra: AD ≈ 9,70 (cm)
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A=90 độ, AB<AC. Kẻ đường cao AH vuông góc với BC. Kẻ AD là phân giác góc HAC. Kẻ BE là đường phân giác góc ABC. CMR BE vuông góc với AD
cac ban oi giup minh nhe
Goi F la giao diem cua BE va AH, I la giao diem cua BE va AD
ta co: goc ABC+ goc ACB=90 ( tam giac ABC vuong tai A)
goc HAC+ goc ACB=90 ( tam giac AHC vuong tai H)
===> goc ABC= goc HAC
ta co : goc HAD=1/2 goc HAC ( AD la tia p/g goc HAC)
goc FBH=1/2 goc ABC ( BE la tia p/g goc ABC )
goc ABC= goc HAC ( cmt)
--> goc HAD= goc FBH
ta co: goc BFH+ goc FBH =90 ( tam giac FBH vuong tai H)
goc FBH= goc HAD ( cmt)
goc BFH= goc AFI ( 2 goc doi dinh)
===> goc HAD+ goc AFI =90 hay goc FAI+ goc AFI=90
xet tam giac AFI ta co: goc AFI+ gic FAI+ goc AIF=180 ( tong 3 goc trong tamgiac )
ma goc AFI+ goc FAI =90 ( cmt )
nen 90+ goc AIF =180
--> goc AIF =180-90=90
--> AI vuong goc FI hay BE vuong goc AD tai I
Đúng 0
Bình luận (0)
cho tam gics ABC biết góc B> góc C . kẻ đường cao AH và phân giác AD,
a) CMR :GÓC HAD = GÓC B - GÓC C / 2














