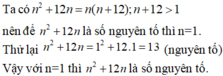Tìm n thuộc N để n2 + 12n là số nguyên tố
Những câu hỏi liên quan
24 tháng 2 2023 lúc 23:42
Tìm n ϵ N để n2 + 12n là số nguyên tố
Lời giải:
$n^2+12n=n(n+12)$ nên để $n^2+12n$ là số nguyên tố thì 1 trong 2 thừa số $n, n+12$ bằng $1$, số còn lại là số nguyên tố.
Mà $n< n+12$ nên $n=1$
Khi đó: $n^2+12n=1^2+12.1=13$ là số nguyên tố (thỏa mãn)
Đúng 5
Bình luận (0)
Tìm tất cả các số tự nhiên n để
n
2
+
12
n
là số nguyên tố. A. n11 B. n13 C. n2 D. n1
Đọc tiếp
Tìm tất cả các số tự nhiên n để n 2 + 12 n là số nguyên tố.
A. n=11
B. n=13
C. n=2
D. n=1
tìm n thuộc N để n^4-6n^3+12n^2-12n+20 là số nguyên tố
tìm n thuộc N để:
a) m^2 +12n là số nguyên tố
b) 3^n+6 là số nguyên tố
^ là mũ
tìm n thuộc N để n3+n2-n+2 là số nguyên tố
Tìm tất cả các số tự nhiên n để :
a/ n^2 +12n là số nguyên tố
b/ 3^n +6 là số nguyên tố
Tìm tất cả các số tự nhiên n để :
a/ n^2 +12n là số nguyên tố
b/ 3^n +6 là số nguyên tố
Đúng 0
Bình luận (0)
Tìm tất cả STN n để:
a)n2+12n là số nguyên tố
b)3n+6 là số nguyên tố
Tìm n để A= 12n^2 - 5n -25 là số nguyên tố
Tìm số tự nhiên n để n2+12n là 1 số nguyên tố
Ta có:
Gọi A=n^2+12n=n.n+12n=(12+n).n
=> 12+n và n là ước của A
Vì A là 1 số nguyên tố nên A chỉ có 2 ước trong đó có 1 và cũng là 2 ước 12+n và n
=> 1 trong 2 ước 12+n và n bằng 1
12+n không thể bằng 1 vì n là số tự nhiên nên kết quả 12+n bé nhất là 12 (12+0)
=> n=1.
Đúng 0
Bình luận (0)