Trong 1buổi học .Yên ra bài toán đố cho Bình:nếu 1\(\Delta\) độ dài 2 đường cao là 3^2;5^2 và đường cao thứ ba cũng là số chính phương thì đường cao thứ 3 là bao nhiêu ?

Những câu hỏi liên quan
Trong 1 buổi học nhóm, Yên ra bài toán đố Bình: "Nếu một tam giác có độ dài hai đường cao là 3^2, 5^2 và đường cao thứ 3 cũng là số chính phương thì đường cao thứ 3 là bao nhiêu ?" . Em hãy giải bài toán giúp Bình
trong 1 buổi học nhóm yến ra 1 bài toán đó bình;nếu 1 tam giác có độ dài 2 đường cao là 9 và 25 và đường cao thứ 3 cũng là 1 số chính phương thì đường cao thứ 3 bằng bao nhiêu em hãy giải bài toán này giúp bình
Toán kham khảo nha các bạn học sinh giỏi :
Bài 1:(1đ)
Cho Delta ABC có các đường cao BM ; CN cắt nhau tại H . Kẻ A với H cắt BC tại E . Chứng minh rằng : MH là tia phân giác của góc NME .
Bài 2 : (3đ)
Cho Delta ABC nhọn ; các đường cao AABBCC cắt nhau tại H
1) Tính tổng : dfrac{HA}{AA}+dfrac{HB}{BB}+dfrac{HC}{CC} .
2) Chứng minh rằng : BH.BB+CH.CCBC^2
3) Chứng minh rằng : AH.AA+CH.CC+BH.BBdfrac{AB^2+AC^2+CB^2}{2}
4) Gọi AI là tia phân giác của Delta ABC ; IM và IN theo thứ tự là phân giá...
Đọc tiếp
Toán kham khảo nha các bạn học sinh giỏi :
Bài 1:(1đ)
Cho \(\Delta ABC\) có các đường cao BM ; CN cắt nhau tại H . Kẻ A với H cắt BC tại E . Chứng minh rằng : MH là tia phân giác của góc NME .
Bài 2 : (3đ)
Cho \(\Delta ABC\) nhọn ; các đường cao AA'BB'CC' cắt nhau tại H
1) Tính tổng : \(\dfrac{HA'}{AA'}+\dfrac{HB'}{BB'}+\dfrac{HC'}{CC'}\) .
2) Chứng minh rằng : \(BH.BB'+CH.CC'=BC^2\)
3) Chứng minh rằng : \(AH.AA'+CH.CC'+BH.BB'=\dfrac{AB^2+AC^2+CB^2}{2}\)
4) Gọi AI là tia phân giác của \(\Delta ABC\) ; IM và IN theo thứ tự là phân giác của góc AIC và góc AIB . Chứng minh rằng : \(\sqrt{AN.BI.CM}=\sqrt{BN.IC.AM}\)
Đố vui tí:
Nếu 1 tam giác có độ dài 2 đường cao là \(3^2,5^2\) và đường cao thứ 3 cũng là số chính phương thì độ dài đường cao thứ 3 là bao nhiêu?
Gọi độ dài 3 cạnh của tam giác lần lượt là a,b,c khi đó độ dài đường cao tương ứng là 9,25,m trong đó:\(a,b,c\)là các số thực dương và \(m\in N\)
Theo đề ra,ta có:
\(9a=25b=2S\)(S là diện tích tam giác)
\(\Rightarrow a=\frac{2S}{9},b=\frac{2S}{25},c=\frac{2S}{m}\)
Áp dụng BĐT tam giác ta có:\(a-b< c< a+b\)
\(\Rightarrow\frac{225}{34}< m< \frac{225}{16}\)
\(\Rightarrow m=9\)vì m là số chính phương.
P/S:nếu có lỗi gì đó không nghiêm trọng đến mức sai bài giải,mong mọi người bỏ qua cho.
Đúng 0
Bình luận (0)
Ủa mk tưởng tam giác vuông là trường hợp đặc biệt cũng chỉ có 2 đường cao thôi mà ? ???
Đúng 0
Bình luận (0)
Tam giác vuông vẫn có 3 đường cao mà :vv chỉ là nó ở bên ngoài thôi, tức là mình phải kéo dài ra ý
Đúng 0
Bình luận (0)
bài 1: Trong tam giác vuông với các cạnh góc vuông có độ dài là 3 và 4,kẻ đường cao tương ứng vs cạnh huyền .Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền
bài 2: Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2.Hãy tính các cạnh góc vuông của tam giác này
AI GIÚP VS HELP ME CẦN GẤP
Bài 1:
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)
Đúng 0
Bình luận (0)
Bài 2:
Ta có: △ABC vuông tại A và có đg cao AH
AB2 = BH.BC ( hệ thức lượng )
⇒ x2 = 1 . 3
⇒ x = \(\sqrt{1.3}=\sqrt{3}cm\)
AC2 = CH.BC
⇒ y2 = 2 . 3
⇒ y = \(\sqrt{6}\) cm
Đúng 0
Bình luận (0)
bài 1 : toán đốsố học sinh khối 6 của một trường khi xếp thành 12 hàng, 15 hàng, 18 hàng đều dư ra 9 học sinh. Tìm số học sinh khối 6 của trường biết số đó lớn hơn 300 và nhỏ hơn 400bài 2 : toán đố Một miếng vườn hình chữ nhật, chiều dài 105m, chiều rộng 60m. Người ta muốn trồng cây xung quanh sao cho mỗi góc vườn một cây và khoảng cách giữa hai cây liên tiếp là bằng nhau. Tính khoảng cách lớn nhất của hai cây bài 3: toán đốMột khối học sinh khi xếp hàng 2, hàng 3, hàng 4 , hàng 5, hàng 6 đều th...
Đọc tiếp
bài 1 : toán đố
số học sinh khối 6 của một trường khi xếp thành 12 hàng, 15 hàng, 18 hàng đều dư ra 9 học sinh. Tìm số học sinh khối 6 của trường biết số đó lớn hơn 300 và nhỏ hơn 400
bài 2 : toán đố
Một miếng vườn hình chữ nhật, chiều dài 105m, chiều rộng 60m. Người ta muốn trồng cây xung quanh sao cho mỗi góc vườn một cây và khoảng cách giữa hai cây liên tiếp là bằng nhau. Tính khoảng cách lớn nhất của hai cây
bài 3: toán đố
Một khối học sinh khi xếp hàng 2, hàng 3, hàng 4 , hàng 5, hàng 6 đều thiếu 1 người, nhưng xếp hàng 7 thì vừa đủ. Biết số học sinh chưa đến 300. Tính số học sinh
Bài 1: Gọi số học sinh của khối 6 là a. Theo bài ta có : a = 12k+9 = 15k+9 = 18k+9 và 300<a<400 Suy ra a-9 chia hết cho 12; 15; 18 và 300<a<400 Hay a-9 \(\in\) BC(12;15;18) và 291<a<391 (1) Ta có 12 = 22. 3
15=3.5
18=2.32
Suy ra BCNN(12;15;18) = 22.32.5= 180
BC(12;15;18) = { 0; 180;360;540;....} (2)
Từ (1) và (2) suy ra a-9 = 360
Vì a-9 = 360 nên a = 360 + 9= 369
Vậy khối 6 có tất cả 369 học sinh!!!!!
Đúng 0
Bình luận (0)
Đố: Cho \(\Delta ABC\)có độ dài các cạnh AB, BC, AC lần lượt là 3 số tự nhiên liên tiếp tăng dần. Kẻ đường cao AH, trung tuyến AM. Tính HM.
Đặt AB = x , BC = x + 1 , AC = x + 2 , MH = a Xét 3 trường hợp
Trường hợp 1 nếu góc B < 90o => BC > AC (khác đề)
Trường hợp 2 nếu góc B = 90 độ (khác đề)
Trường hợp 3 nếu góc B > 90o => AC > BC ( đúng)
Nên ta sẽ đi xét trường hợp 3 : B > 90o ( bạn phải vẽ B > 90o nhé) HB = MH - BM
=> HB = a - (x+1)/2
=> HB^2 = (a - (x+1)/2)^2 HC = HB + BC
=> HC = a - x/2 + x
=> HC^2 = (a + (x+1)/2)^2
Ta có AH^2 = AC^2 - HC^2 AH^2 = AB^2 - HB^2
=> AC^2 - HC^2 = AB^2 - HB^2
<=> (x + 2)^2 - (a+ (x+1)/2)^2 = x^2 - (a - (x+1)/2)^2
<=> x^2 - 4x - 4 - a^2 - ax - a - (x^2+2x+1)/4 = x^2 - a^2 + ax + a - (x^2+2x+1)/4
<=> 2ax + 2a - 4x - 4 = 0
<=> 2a(x+1) - 4(x+1) = 0
<=> (x + 1).2(a - 2) = 0
<=> x = -1 hoặc a = 2 hay AB = -1 hoặc HM = 2
Hai cạnh của một hình bình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp án ?
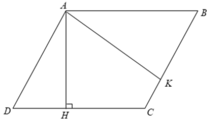
Xét hình bình bình ABCD có AB = CD = 8( cm ) và AD = BC = 6( cm )
Từ A kẻ các đường cao AH,AK.
Khi đó ta có:
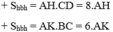
Mà một hình bình hành thì chỉ có một diện tích chung nên 8.AH = 6.AK
Nếu độ dài đường cao thứ nhất là AH = 5( cm ) thì:
8.5 = 6.AK ⇔ AK = (8.5)/6 = 20/3( cm ) là độ dài đường cao thứ hai.
Nếu độ dài đường cao thứ nhất là AK = 5( cm ) thì:
8.AH = 6.5 ⇔ AH = (6.5)/8 = 15/4( cm ) là độ dài đường cao thứ hai.
Vậy bài toán này có hai đáp số
Đúng 0
Bình luận (0)
Hai cạnh của một hình bình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp án ?
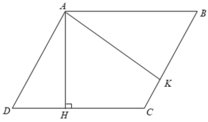
Xét hình bình bình ABCD có AB = CD = 8( cm ) và AD = BC = 6( cm )
Từ A kẻ các đường cao AH,AK.
Khi đó ta có:
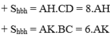
Mà một hình bình hành thì chỉ có một diện tích chung nên 8.AH = 6.AK
Nếu độ dài đường cao thứ nhất là AH = 5( cm ) thì:
8.5 = 6.AK ⇔ AK = (8.5)/6 = 20/3( cm ) là độ dài đường cao thứ hai.
Nếu độ dài đường cao thứ nhất là AK = 5( cm ) thì:
8.AH = 6.5 ⇔ AH = (6.5)/8 = 15/4( cm ) là độ dài đường cao thứ hai.
Vậy bài toán này có hai đáp số
Đúng 0
Bình luận (0)



















