Ba người cùng đi, bảy người hiếm có
Năm cây hoa mai, hai mốt cành nhỏ.
Bảy con đoàn tụ đúng vào ngày rằm.
Để mà biết rõ cộng (trừ) trăm linh năm.
Những câu hỏi liên quan
Ba người cùng đi, bảy mươi hiếm có
Năm cây hoa mai, hâm mốt cành nhỏ
Bảy con đoàn tụ, đúng vào ngày rằm
Để mà biết rõ,cộng (trừ) trăm linh năm
Bài toán “Hàn Tín điểm binh”: Hàn Tín là một vị tướng nhà Hán, Trung Quốc. Ông có cách điểm binh rất tài tình; muốn biết số quân chính xác là bao nhiêu ông cho lần lượt phất ba lá cờ màu khác nhau, quân lính cừ theo màu cờ quy ước mà lần lượt xếp hàng 3, 5, 7 rồi báo cho cho ông biết số người thừa. Gọi số người thừa là a, b, c thì số quân bằng: 79a + 21b + 15c ± B(105). Muốn cho dễ nhớ ông đặt thành thơ:“Ba người cùng đội 70 rànhNăm khóm hoa mai, hăm mốt cànhBảy gã vườn đào chơi nửa thángCộng ho...
Đọc tiếp
Bài toán “Hàn Tín điểm binh”: Hàn Tín là một vị tướng nhà Hán, Trung Quốc. Ông có cách điểm binh rất tài tình; muốn biết số quân chính xác là bao nhiêu ông cho lần lượt phất ba lá cờ màu khác nhau, quân lính cừ theo màu cờ quy ước mà lần lượt xếp hàng 3, 5, 7 rồi báo cho cho ông biết số người thừa. Gọi số người thừa là a, b, c thì số quân bằng: 79a + 21b + 15c ± B(105). Muốn cho dễ nhớ ông đặt thành thơ:
“Ba người cùng đội 70 rành
Năm khóm hoa mai, hăm mốt cành
Bảy gã vườn đào chơi nửa tháng
Cộng hoặc trừ trăm linh năm tính nhẩm nhanh”.
b) Giải thích công thức trên của Hàn Tín
b)
Gọi số quân là n
n=3x+a => 70n=219x+70a
n=5y+b => 21n=105y+21b
n=7z+c => 15n=105z+15c
Do đó: 106n = 70a +21b + 15c ± 105t (t ∈N)
Vậy n = 70a + 21b + 10c ± 105h (h ∈N)
Đúng 0
Bình luận (0)
三 人 同 行 七 十 嬉 五 樹 梅 花 廿 一 枝 七 子 桃 園 秋 半 月 共 除 百 零 五 定 為 其Tam nhân đồng hành thất thập hy, Ngũ thụ mai hoa trấp nhất chi, Thất tử đào viên thu bán nguyệt, Cọng (cộng) trừ bách linh ngũ, định vi kỳ.Tạm dịch :Ba người cùng đi đường, thì vui gấp bảy mươi lần, Năm cây hoa Mai có hai mươi mốt nhánh, Bảy chàng dạo chơi vườn Đào vào giữa tháng của mùa Thu, Thêm hay bớt một trăm lẻ năm để định đáp số.
Đọc tiếp
三 人 同 行 七 十 嬉
五 樹 梅 花 廿 一 枝
七 子 桃 園 秋 半 月
共 除 百 零 五 定 為 其
Tam nhân đồng hành thất thập hy,
Ngũ thụ mai hoa trấp nhất chi,
Thất tử đào viên thu bán nguyệt,
Cọng (cộng) trừ bách linh ngũ, định vi kỳ.
Tạm dịch :
Ba người cùng đi đường, thì vui gấp bảy mươi lần,
Năm cây hoa Mai có hai mươi mốt nhánh,
Bảy chàng dạo chơi vườn Đào vào giữa tháng của mùa Thu,
Thêm hay bớt một trăm lẻ năm để định đáp số.
Ý bài nầy là " Tôn Tử " biết chừng chừng số binh của mình. Muốn biết số binh chính xác, thì :
- Làm dấu hiệu thứ nhất -ph ất một lần cây cờ - thì cứ 3 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1 hoặc 2 người ; số nầy sẽ nhân với 70.
- Làm dấu hiệu thứ hai, thì cứ 5 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1, 2, 3 hoặc 4 người ; số nầy sẽ nhân cho 21.
- Làm dấu hiệu thứ ba, thì cứ 7 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1, 2, 3, 4, 5 hoặc 6 người ; số nầy sẽ nhân cho 15.
Cọng tất cả 3 số vừa được nhân ở trên, và nếu cần thì cọng thêm, hoặc trừ ra 105, để được số binh chính xác.).
Ví dụ : Số binh là 437, và " Tôn Tử " biết chừng chừng là khoảng 400.
- Nếu sắp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu sắp 5 người thành một nhóm, thì lẻ ra 2 người,
- Nếu sắp 7 người thành một nhóm, thì lẻ ra 3 người.
Và : (2 x 70) + (2 x 21) + (3 x 15) + 105 + 105 = (140 + 42 + 45) + 210 = 227 + 210 = 437.
Cái hay ở đây là chỉ dùng có 3 động tác đơn sơ và chỉ trong vài ba phút mà " Tôn Tử " đã biết được số binh chính xác của mình.
Chuyện bài toán trên là Phép Chia Euclide (1) về Số Học trong Tập Hợp Số Nguyên Z. Vậy ta có thể thay những số 3, 5, 7; 70, 21, 15; 105, trên, bằng những nhóm số khác như 2, 3, 5; 15, 10, 6; 30; hay 3, 5, 11; 55, 66, 45; 165 ; vân vân, nhưng theo tôi nhóm số 3, 5, 7; 70, 21, 15; 105 trên vẫn đơn giản hơn nhiều.
Ví dụ với nhóm số 2, 3, 5; 15, 10, 6; 30 :
Cũng lấy số binh trên 437.
- Nếu xếp 2 người thành một nhóm, thì lẻ ra 1 người,
- Nếu xếp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu xếp 5 người thành một nhóm, thì lẻ ra 2 người.
Và (1 x 15) + (2 x 10) + (2 x 6) + (13 x 30) = (15 + 20 + 12) + 390 = 47 + 390 = 437.
Ở đây 47 phải cọng thêm 13 lần 30, (13 x 30 = 390).
Đúng 0
Bình luận (0)
Bài toán “Hàn Tín điểm binh”: Hàn Tín là một vị tướng nhà Hán, Trung Quốc. Ông có cách điểm binh rất tài tình; muốn biết số quân chính xác là bao nhiêu ông cho lần lượt phất ba lá cờ màu khác nhau, quân lính cừ theo màu cờ quy ước mà lần lượt xếp hàng 3, 5, 7 rồi báo cho cho ông biết số người thừa. Gọi số người thừa là a, b, c thì số quân bằng: 79a + 21b + 15c ± B(105). Muốn cho dễ nhớ ông đặt thành thơ:“Ba người cùng đội 70 rànhNăm khóm hoa mai, hăm mốt cànhBảy gã vườn đào chơi nửa thángCộng ho...
Đọc tiếp
Bài toán “Hàn Tín điểm binh”: Hàn Tín là một vị tướng nhà Hán, Trung Quốc. Ông có cách điểm binh rất tài tình; muốn biết số quân chính xác là bao nhiêu ông cho lần lượt phất ba lá cờ màu khác nhau, quân lính cừ theo màu cờ quy ước mà lần lượt xếp hàng 3, 5, 7 rồi báo cho cho ông biết số người thừa. Gọi số người thừa là a, b, c thì số quân bằng: 79a + 21b + 15c ± B(105). Muốn cho dễ nhớ ông đặt thành thơ:
“Ba người cùng đội 70 rành
Năm khóm hoa mai, hăm mốt cành
Bảy gã vườn đào chơi nửa tháng
Cộng hoặc trừ trăm linh năm tính nhẩm nhanh”.
a) Em hãy áp dụng công thức Hàn Tín để giải bài toán sau: Số học sinh tham dự giải thưởng Lương Thế Vinh vào khoảng năm 4600 đến 4700 học sinh, biết rằng nếu xếp hàng 3 dư 2, hàn 5 dư 3 và hàng 7 dư 4. Tính số học sinh tham dự.
Bài toán “Hàn Tín điểm binh”: Hàn Tín là một vị tướng nhà Hán, Trung Quốc. Ông có cách điểm binh rất tài tình; muốn biết số quân chính xác là bao nhiêu ông cho lần lượt phất ba lá cờ màu khác nhau, quân lính cừ theo màu cờ quy ước mà lần lượt xếp hàng 3, 5, 7 rồi báo cho cho ông biết số người thừa. Gọi số người thừa là a, b, c thì số quân bằng: 79a + 21b + 15c ± B(105). Muốn cho dễ nhớ ông đặt thành thơ:“Ba người cùng đội 70 rànhNăm khóm hoa mai, hăm mốt cànhBảy gã vườn đào chơi nửa thángCộng ho...
Đọc tiếp
Bài toán “Hàn Tín điểm binh”: Hàn Tín là một vị tướng nhà Hán, Trung Quốc. Ông có cách điểm binh rất tài tình; muốn biết số quân chính xác là bao nhiêu ông cho lần lượt phất ba lá cờ màu khác nhau, quân lính cừ theo màu cờ quy ước mà lần lượt xếp hàng 3, 5, 7 rồi báo cho cho ông biết số người thừa. Gọi số người thừa là a, b, c thì số quân bằng: 79a + 21b + 15c ± B(105). Muốn cho dễ nhớ ông đặt thành thơ:
“Ba người cùng đội 70 rành
Năm khóm hoa mai, hăm mốt cành
Bảy gã vườn đào chơi nửa tháng
Cộng hoặc trừ trăm linh năm tính nhẩm nhanh”.
a) Em hãy áp dụng công thức Hàn Tín để giải bài toán sau: Số học sinh tham dự giải thưởng Lương Thế Vinh vào khoảng năm 4600 đến 4700 học sinh, biết rằng nếu xếp hàng 3 dư 2, hàn 5 dư 3 và hàng 7 dư 4. Tính số học sinh tham dự.
b) Giải thích công thức trên của Hàn Tín
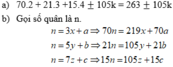
Do đó: 106n = 70a +21b + 15c ± 105t (t ∈N)
Vậy n = 70a + 21b + 10c ± 105h (h ∈N)
Đúng 0
Bình luận (0)
Hay bài giai thoại Điểm Binh của Tôn Tử :三 人 同 行 七 十 嬉 五 樹 梅 花 廿 一 枝 七 子 桃 園 秋 半 月 共 除 百 零 五 定 為 其Tam nhân đồng hành thất thập hy, Ngũ thụ mai hoa trấp nhất chi, Thất tử đào viên thu bán nguyệt, Cọng (cộng) trừ bách linh ngũ, định vi kỳ.Tạm dịch :Ba người cùng đi đường, thì vui gấp bảy mươi lần, Năm cây hoa Mai có hai mươi mốt nhánh, Bảy chàng dạo chơi vườn Đào vào giữa tháng của mùa Thu, Thêm hay bớt một trăm lẻ năm để định đáp số. ...
Đọc tiếp
Hay bài giai thoại " Điểm Binh của Tôn Tử " :
三 人 同 行 七 十 嬉
五 樹 梅 花 廿 一 枝
七 子 桃 園 秋 半 月
共 除 百 零 五 定 為 其
Tam nhân đồng hành thất thập hy,
Ngũ thụ mai hoa trấp nhất chi,
Thất tử đào viên thu bán nguyệt,
Cọng (cộng) trừ bách linh ngũ, định vi kỳ.
Tạm dịch :
Ba người cùng đi đường, thì vui gấp bảy mươi lần,
Năm cây hoa Mai có hai mươi mốt nhánh,
Bảy chàng dạo chơi vườn Đào vào giữa tháng của mùa Thu,
Thêm hay bớt một trăm lẻ năm để định đáp số.
Tôi để hai chữ " Tôn Tử " trong dấu ngoặc kép, vì tôi không có tài liệu nào trong tay để quyết đoán bài thơ " Điểm Binh " trên là của Tôn Tử.
(Ý bài nầy là " Tôn Tử " biết chừng chừng số binh của mình. Muốn biết số binh chính xác, thì :
- Làm dấu hiệu thứ nhất - như phất một lần cây cờ - thì cứ 3 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1 hoặc 2 người ; số nầy sẽ nhân với 70.
- Làm dấu hiệu thứ hai, thì cứ 5 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1, 2, 3 hoặc 4 người ; số nầy sẽ nhân cho 21.
- Làm dấu hiệu thứ ba, thì cứ 7 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1, 2, 3, 4, 5 hoặc 6 người ; số nầy sẽ nhân cho 15.
Cọng tất cả 3 số vừa được nhân ở trên, và nếu cần thì cọng thêm, hoặc trừ ra 105, để được số binh chính xác.).
Ví dụ : Số binh là 437, và " Tôn Tử " biết chừng chừng là khoảng 400.
- Nếu sắp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu sắp 5 người thành một nhóm, thì lẻ ra 2 người,
- Nếu sắp 7 người thành một nhóm, thì lẻ ra 3 người.
Và : (2 x 70) + (2 x 21) + (3 x 15) + 105 + 105 = (140 + 42 + 45) + 210 = 227 + 210 = 437.
Cái hay ở đây là chỉ dùng có 3 động tác đơn sơ và chỉ trong vài ba phút mà " Tôn Tử " đã biết được số binh chính xác của mình.
Chuyện bài toán trên là Phép Chia Euclide (1) về Số Học trong Tập Hợp Số Nguyên Z. Vậy ta có thể thay những số 3, 5, 7; 70, 21, 15; 105, trên, bằng những nhóm số khác như 2, 3, 5; 15, 10, 6; 30; hay 3, 5, 11; 55, 66, 45; 165 ; vân vân, nhưng theo tôi nhóm số 3, 5, 7; 70, 21, 15; 105 trên vẫn đơn giản hơn nhiều.
Ví dụ với nhóm số 2, 3, 5; 15, 10, 6; 30 :
Cũng lấy số binh trên 437.
- Nếu xếp 2 người thành một nhóm, thì lẻ ra 1 người,
- Nếu xếp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu xếp 5 người thành một nhóm, thì lẻ ra 2 người.
Và (1 x 15) + (2 x 10) + (2 x 6) + (13 x 30) = (15 + 20 + 12) + 390 = 47 + 390 = 437.
Ở đây 47 phải cọng thêm 13 lần 30, (13 x 30 = 390).
Đúng 0
Bình luận (0)
Tôi để hai chữ " Tôn Tử " trong dấu ngoặc kép, vì tôi không có tài liệu nào trong tay để quyết đoán bài thơ " Điểm Binh " trên là của Tôn Tử.
(Ý bài nầy là " Tôn Tử " biết chừng chừng số binh của mình. Muốn biết số binh chính xác, thì :
- Làm dấu hiệu thứ nhất - như phất một lần cây cờ - thì cứ 3 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1 hoặc 2 người ; số nầy sẽ nhân với 70.
- Làm dấu hiệu thứ hai, thì cứ 5 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1, 2, 3 hoặc 4 người ; số nầy sẽ nhân cho 21.
- Làm dấu hiệu thứ ba, thì cứ 7 người lính đứng lại thành một nhóm, số lính còn lại không lập được một nhóm là 0, 1, 2, 3, 4, 5 hoặc 6 người ; số nầy sẽ nhân cho 15.
Cọng tất cả 3 số vừa được nhân ở trên, và nếu cần thì cọng thêm, hoặc trừ ra 105, để được số binh chính xác.).
Ví dụ : Số binh là 437, và " Tôn Tử " biết chừng chừng là khoảng 400.
- Nếu sắp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu sắp 5 người thành một nhóm, thì lẻ ra 2 người,
- Nếu sắp 7 người thành một nhóm, thì lẻ ra 3 người.
Và : (2 x 70) + (2 x 21) + (3 x 15) + 105 + 105 = (140 + 42 + 45) + 210 = 227 + 210 = 437.
Cái hay ở đây là chỉ dùng có 3 động tác đơn sơ và chỉ trong vài ba phút mà " Tôn Tử " đã biết được số binh chính xác của mình.
Chuyện bài toán trên là Phép Chia Euclide (1) về Số Học trong Tập Hợp Số Nguyên Z. Vậy ta có thể thay những số 3, 5, 7; 70, 21, 15; 105, trên, bằng những nhóm số khác như 2, 3, 5; 15, 10, 6; 30; hay 3, 5, 11; 55, 66, 45; 165 ; vân vân, nhưng theo tôi nhóm số 3, 5, 7; 70, 21, 15; 105 trên vẫn đơn giản hơn nhiều.
Ví dụ với nhóm số 2, 3, 5; 15, 10, 6; 30 :
Cũng lấy số binh trên 437.
- Nếu xếp 2 người thành một nhóm, thì lẻ ra 1 người,
- Nếu xếp 3 người thành một nhóm, thì lẻ ra 2 người,
- Nếu xếp 5 người thành một nhóm, thì lẻ ra 2 người.
Và (1 x 15) + (2 x 10) + (2 x 6) + (13 x 30) = (15 + 20 + 12) + 390 = 47 + 390 = 437.
Ở đây 47 phải cọng thêm 13 lần 30, (13 x 30 = 390).
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Viết số vào chỗ chấm (theo mẫu):
Năm trăm bảy mươi mốt: 571
Sáu trăm hai mươi lăm: ………
Một trăm mười sáu: ………
Bốn trăm năm mươi: ………
Tám trăm ba mươi tư: ………
Ba trăm linh bảy: ………
Sáu trăm hai mươi lăm: 625
Một trăm mười sáu: 116
Bốn trăm năm mươi: 450
Tám trăm ba mươi tư: 834
Ba trăm linh bảy: 307
Đúng 0
Bình luận (0)
Viết vào ô trống (theo mẫu) :
Viết số
Đọc số
21 305 687
Hai mươi mốt triệu ba trăm linh năm nghìn sáu trăm tám mươi bảy
5 978 600
Năm trăm triệu ba trăm linh tám nghìn
Một tỉ tám trăm bảy mươi hai triệu
Đọc tiếp
Viết vào ô trống (theo mẫu) :
| Viết số | Đọc số |
| 21 305 687 | Hai mươi mốt triệu ba trăm linh năm nghìn sáu trăm tám mươi bảy |
| 5 978 600 | |
| Năm trăm triệu ba trăm linh tám nghìn | |
| Một tỉ tám trăm bảy mươi hai triệu |
| Viết số | Đọc số |
| 21 305 687 | Hai mươi mốt triệu ba trăm linh năm nghìn sáu trăm tám mươi bảy |
| 5 978 600 | Năm triệu chín trăm bảy mươi tám nghìn sáu trăm đồng |
| 500 308 000 | Năm trăm triệu ba trăm linh tám nghìn |
| 1 872 000 000 | Một tỉ tám trăm bảy mươi hai triệu |
Đúng 0
Bình luận (0)
Dễ mà ❤️❤️❤️❤️ chuk bạn học giỏi
Viết các số sau:
Sáu trăm mười ba triệu.
Một trăm ba mươi mốt triệu bốn trăm linh năm nghìn.
Năm trăm mười hai triệu ba trăm hai mươi sáu nghìn một trăm linh ba.
Tám mươi sáu triệu không trăm linh bốn nghìn bảy trăm linh hai.
Tám trăm triệu không trăm linh bốn nghìn bảy trăm hai mươi.
613000000
131405000
512326103
86004702
800004720
Đúng 1
Bình luận (0)