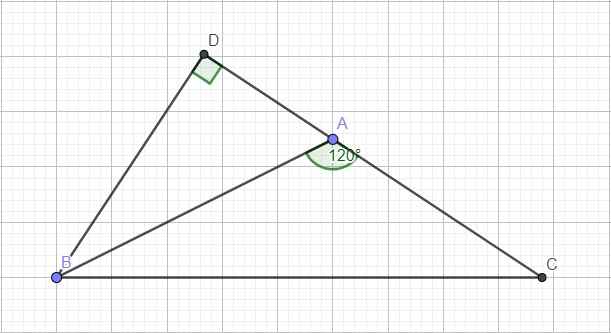
cho tam giác ABC có B=120,BC=c,AC=b.tinh BC theo b,c

Những câu hỏi liên quan
Cho tam giác ABC có A=120 độ, BC=a;AC=b;AB=c . CMR a^2=b^2+c^2+bc
Cho tam giác ABC có góc A =120 độ AC= b AB=c BC=a
CMR: a^2=b^2 +c^2 +bc
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
Đúng 3
Bình luận (0)
Tam giác ABC có Â=120 độ . BC = a; AC=b; AB =c Cm rằng: a^2=b^2+c^2+bc
Cho tam giác ABC có góc A = 120o, BC = a , AC= b, AB= c. Chứng minh rằng a^2 = b^2 +c^2+bc
Kẻ CE vuông góc với AB, ta có ngay tam giác ACE vuông có một góc nhọn 60. Suy ra \(AE=\frac{1}{2}AC=\frac{b}{2},CE=\frac{\sqrt{3}}{2}b\). Xét tam giác vuông EBC có '\(EB=c+\frac{b}{2},EC=\frac{\sqrt{3}}{2}b\to a^2=BC^2=BE^2+CE^2=\left(c+\frac{b}{2}\right)^2+\left(\frac{\sqrt{3}}{2}b\right)^2=c^2+bc+b^2\)
Đúng 0
Bình luận (0)
đáp án
=c2 + bc + b2
hok tót
Đúng 0
Bình luận (0)
trả lời
= c2+ bc + b2
hok tốt
Đúng 0
Bình luận (0)
cho tam giác ABC, góc A=120 độ, AB=c, BC=a, AC=b. C/m: a2=b2+c2+bc
Cho tam giác ABC có AB = 5cm, BC = 6cm, AC = 8 cm. Qua các điểm A,B,C kẻ các đường thẳng a,b,c theo thứ tự song song với BC, AC, AB. Giả sử a cắt b,c theo thứ tự tại E,F ; b cắt c tại D . Tính chu vi tam giác ABC, tam giác ABE, tam giác BCD, tam giác ACF, tam giác DEF
.png)
Chu vi tam giác ABC bằng: 5 + 6 + 8 = 19 (cm)
Dễ dàng thấy ngay \(\Delta ABE=\Delta BAC\left(g-c-g\right)\)
Vậy nên \(P_{ABE}=P_{BAC}=19cm.\)
Ta thấy \(\Delta BCD=\Delta CBA\left(g-c-g\right)\)
Vậy nên \(P_{BCD}=P_{CBA}=19cm.\)
Ta thấy \(\Delta ACF=\Delta CAB\left(g-c-g\right)\)
Vậy nên \(P_{ACF}=P_{CBA}=19cm.\)
\(P_{DEF}=DE+EF+FD=2.8+2.6+2.5=38cm.\)
Đúng 0
Bình luận (0)
chị có thể giải chi tiết được không
cho hình tam giác ABC có góc A = 120 độ có BC=a, AC=b, AB= C chứng minh a^2=b^2+c^2+b^2
Cho tam giác ABC có góc A bằng 120 độ, BC=a;AB=c;AC=b
Chứng minh a2=b2+c2+bc