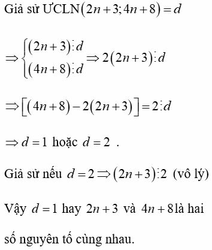gọi \(ƯCLN\left(2n+3;4n+8\right)=d\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\left(4n+8\right)-2\left(2n+3\right)⋮d\Rightarrow2⋮d}\)

\(\Rightarrow d=\left\{1;2\right\}\)

mà 2n+3 là số lẻ; 4n+8 là số chẵn nên d=1 => hai số nguyên tố cùng nhau

 Câu trả lời hay nhất:  Gọi d = (12n + 1 , 30n + 2) 
=> 12n + 1 chia hết cho d và 30n + 2 chia hết cho d 
=> 5(12n + 1) - 2(30n + 2) chia hết cho d 
=> 1 chia hết cho d 
=> d = 1 
=> 12n + 1 và 30n + 2 là hai số nguyên tố cùng nhau

\(\text{Đặt }\left(2n+3,4n+8\right)=d\)

\(\Rightarrow\hept{\begin{cases}\left(2n+3\right)⋮d\\\left(4n+8\right)⋮d\end{cases}}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\\left(4n+8\right)⋮d\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(4n+6\right)⋮d\\\left(4n+8\right)⋮d\end{cases}}\)

\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)=2⋮d\)

\(\Rightarrow d\in\left\{1;2\right\}\)

\(\text{Dễ thấy }d\ne2\)

\(\Rightarrow\left(2n+3,4n+8\right)=1\)

Goi d là ƯCLN ( 2n + 3 ; 4n + 8 )

\(\Rightarrow\) 2n + 3 và 4n + 8 chia hết cho d

\(\Rightarrow\) 2 . ( 2n + 3 ) chia hết cho d

          1 . ( 4n + 8 ) chia hết cho d

\(\Rightarrow\) 4n + 6 chia hết cho d 

           4n + 8 chia hết cho d

\(\Rightarrow\) 4n + 8 - ( 4n + 6 ) chia hết cho d

          4n + 8 - ( 4n - 6 ) chia hết cho d

Suy ra 2 chia hết cho d .

        d € Ư ( 2 ) = { 1 ; 2 }

Mà 2n + 3 không chia hết cho 2 . Suy ra d = 1

\(\Rightarrow\) ƯCLN ( 2n + 3 ; 3n + 4 ) = 1

Vậy 2n + 3 và 3n + 4 là 2 số nguyên tố cùng nhau .

4n+8=2(2n+4)

2n+3,2n+4 ng tố cùng nhau 2 stn liên tiếp

 k mình nha

Giả sử ƯCLN(2n+3 ;4n+8) = d

2 n + 3 ⋮ d 4 n + 8 ⋮ d ⇒ 2 2 n + 3 ⋮ d

=>  4 n + 8 - 2 2 n + 3 = 2 ⋮ d

=>d = 1 hoặc d = 2 .

Giả sử nếu d = 2 => (2n+3) ⋮ 2 (vô lý)

Vậy d = 1 hay 2n+3 và 4n+8 là hai số nguyên tố cùng nhau

Gọi d = UCLN(2n+3,4n+8)

Suy ra 2n+3 ⋮ d và 4n+8 ⋮ d

Ta có 2n+3 ⋮ d => 2.(2n+3) ⋮ d => 4n+6 ⋮ d

Vì 4n+8 ⋮ d và 4n+6 ⋮ d nên (4n+8) – (4n+6) ⋮ d => 2 ⋮ d => d ∈ {1;2}

Vì 2n+3 là số lẻ nên d = 2 là không thỏa mãn. Vậy d = 1

Vậy với mọi số tự nhiên n thì 2n+3 và 4n+8 là nguyên tố cùng nhau

Gọi ước chung của 2n + 3 và 4n + 8 là d

Ta có: \(\left\{{}\begin{matrix}2n+3⋮d\\4n+8⋮d\end{matrix}\right.\)

           \(\left\{{}\begin{matrix}2\left(2n+3\right)⋮d\\4n+8⋮d\end{matrix}\right.\)

            \(\left\{{}\begin{matrix}4n+6⋮d\\4n+8⋮d\end{matrix}\right.\)

             4n + 6 - 4n - 8 ⋮ d

                                  2 ⋮ d

             d \(\in\) Ư(2) = {1; 2)

Nếu d =  2 ⇒ 2n + 3 ⋮ 2 ⇒ 3 ⋮ 2 (vô lí loại)

Vậy d = 1; hay 2n + 3 và 4n + 8 là hai số nguyên tố cùng nhau (đpcm)

Tham Khảo:

Giả sử: \(UCLN\left(2n+3;4n+8\right)=d\)

=> \(\left\{{}\begin{matrix}2n+3⋮d\\4n+8⋮d\end{matrix}\right.\) => \(\left\{{}\begin{matrix}4n+6⋮d\\4n+8⋮d\end{matrix}\right.\)

=> \(2⋮d\) => \(\left[{}\begin{matrix}d=1\\d=2\end{matrix}\right.\)

Có 2n+3 là số lẻ => \(2n+3⋮̸2\)

=> d = 1

=> đpcm

gọi a là ước chung lớn nhất của 2n+1 và 3n+2

do đó a phải là ước của \(2\left(3n+2\right)-3\left(2n+1\right)=1\) do đó a=1

hay 2n+1 và 3n+2 là hai số nguyên tố cùng nhau.

b.gọi b là ước chung lớn nhất của 2n+3 và 4n+5

do đó b phải là ước của \(2\left(2n+3\right)-\left(4n+5\right)=1\)do đó b=1

hay 2n+3 và 4n+5 là hai số nguyên tố cùng nhau