a) \(\left|x-5\right|-\left|x-7\right|=\left|x-5\right|-\left|x-5-2\right|\ge\left|x-5\right|-\left(\left|x-5\right|-2\right)=2\)

Dấu \(=\)khi \(-2\left(x-5\right)\ge0\Leftrightarrow x\le5\).

b) \(\left|125-x\right|+\left|x+65\right|\ge\left|125-x+x+65\right|=190\)

Dấu \(=\)khi \(\left(125-x\right)\left(x+65\right)\ge0\Leftrightarrow-65\le x\le125\).

Ta thấy:      |x-10| >= 0      (1);          |x-10| >= 0        (2)

Cộng 2 bđt cùng chiều (1) và (2) ta được:   |x-10| + |x-10| >= 0    <=>  A= |x-10| + |x-10| -2 >= -2

=> minA = -2  

Dấu đẳng thức xảy ra khi và chỉ khi x=10 và y=-100

 Chắc v!! =)))

a) *Xét x=0

==> Giá trị A=2022!(1)

*Xét 0<x≤2022

==> A=0(2)

*Xét x>2022

==> A≥2022!(3)

Từ (1),(2) và (3) ==> Amin=0 khi0<x≤2022

Mà để xmax ==> x=2022 

Vậy ...

b)B=\(\dfrac{2018+2019+2020}{x-2021}\)=\(\dfrac{6057}{x-2021}\) (Điều kiện x-2021≠0 hay x≠2021)

Để Bmax ==> x-2021 là số tự nhiên nhỏ nhất

Mà x-2021≠0 =>x-2021=1==>x=2022

Khi đó Bmax=6057

Vậy...

BÀI 2:

\(\left|x\right|=11\)\(\Rightarrow\)\(x=\pm11\)

\(\left|y+1\right|=15\)\(\Rightarrow\)\(\orbr{\begin{cases}y+1=15\\y+1=-15\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}y=-14\\y=-16\end{cases}}\)

\(A=\frac{27-12x}{x^2+9}\)

\(A=\frac{x^2-12x+36-x^2-9}{x^2+9}\)

\(A=\frac{\left(x-36\right)^2-\left(x^2+9\right)}{x^2+9}\)

\(A=\frac{\left(x-36\right)^2}{x^2+9}-\frac{x^2+9}{x^2+9}\)

\(A=\frac{\left(x-36\right)^2}{x^2+9}-1\ge-1\forall x\)

Dấu "=" xảy ra \(\Leftrightarrow x=36\)

Chọn A

Hàm số f(x) = (x-6) x 2 + 4  xác định và liên tục trên đoạn [0;3].

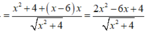
Suy ra 

 với a là số nguyên và b, c là các số nguyên dương nên 

a = - 12, b = 3, c = 13. Do đó: S = a + b + c = 4.

Đáp án B

TXĐ: D=[-2,2]

P'=\(1-\frac{x}{\sqrt{4-x^2}}\)

P'=0<=> \(1-\frac{x}{\sqrt{4-x^2}}=0\)=>\(\hept{\begin{cases}x=\sqrt{4-x^2}\\4-x^2>0\end{cases}}\)

\(\hept{\begin{cases}x^2=4-x^2\\x\ge0\\-2< x< 2\end{cases}}\)

=> \(x=\sqrt{2}\)

P(-2)=-2

\(P\left(\sqrt{2}\right)=2\sqrt{2}\)

P(2)=2

Vậy GTLN của P=\(2\sqrt{2}\),GTNN là -2