Tam giác ABC có góc A = 40o; các đường cao cắt nhau tại H. Khi đó số đo góc BHC bằng

Những câu hỏi liên quan
Tam giác ABC có ∠A = 40o. Các tia phân giác của các góc B và C cắt nhau ở I.
Góc BIC bằng:
(A) 40o;
(B) 70o;
(C) 110o;
(D) 140o.
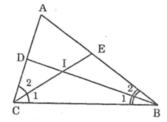
Ta có:
+ Trong ΔBIC có ∠BIC = 180º - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠BAC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠BAC + ∠BCA) (2)
+ Trong ΔABC có: ∠BAC + ∠BCA = 180 - ∠A =140º (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180º - 1/2.140º = 110º
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho tam giác ABC với góc A = 100o, góc B = 40o
Tam giác ABC là tam giác gì?
Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có:
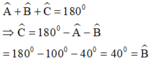
Suy ra ∆ABC cân tại A.
Đúng 0
Bình luận (0)
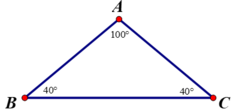
Cho tam giác ABC với góc A = 100o, góc B = 40o.
Tìm cạnh lớn nhất của tam giác ABC.
Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
Đúng 0
Bình luận (0)
Cho tam giác ABC có ∠ A = 40 o . Tia phân giác của góc A cắt BC tại I. Khi đó số đo góc (BAI) là:
A. 20 °
B. 30 °
C. 40 °
D. 35 °
Ta có AI là tia phân giác của góc A nên ∠(BAI) = 40o:2=20o. Chọn A
Đúng 0
Bình luận (0)
Cho tam giác ABC có ∠ A = 40 o . Tia phân giác của góc A cắt BC tại I. Khi đó số đo góc (BAI) là:
A. 20 °
B. 30 °
C. 40 °
D. 35 °
Ta có AI là tia phân giác của góc A nên ∠(BAI) = 40o:2=20o. Chọn A
Đúng 0
Bình luận (0)
Tam giác ABC có
A
^
100
o
,
B
^
-
C
^
40
o
. Số đo góc B và góc C lần lượt là: A.
B
^
60
°
,
C
^
20
°
B.
B
^...
Đọc tiếp
Tam giác ABC có A ^ = 100 o , B ^ - C ^ = 40 o . Số đo góc B và góc C lần lượt là:
A. B ^ = 60 ° , C ^ = 20 °
B. B ^ = 20 ° , C ^ = 60 °
C. B ^ = 70 ° , C ^ = 20 °
D. B ^ = 80 ° , C ^ = 30 °
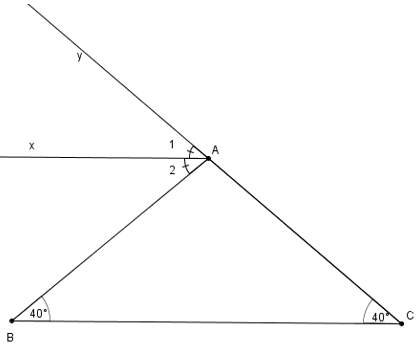
Cho tam giác ABC có góc B = góc C = 40o. Gọi Ax là tia phân giác của góc ngoài đỉnh A. Hãy chứng tó Ax // BC.
Ta có: BAy=B+C (góc ngoài của tam giác)
BAy=400+400=800
Ax là p/g của BAy
⇒ A1=A2=400
Ta có: A2=B=400
Mà hai góc này ở vị trí SLT
⇒ BC//Ax
Đúng 1
Bình luận (0)
Ta có: BAy=B+C (góc ngoài của tam giác)
BAy=400+400=800
Ax là p/g của BAy
⇒ A1=A2=400
Ta có: A2=B=400
Mà hai góc này ở vị trí SLT
⇒ BC//Ax
Đúng 1
Bình luận (0)
Cho tam giác ABC có góc B = góc C = 40o. Gọi Ax là tia phân giác của góc ngoài đỉnh A. Hãy chứng tó Ax // BC.
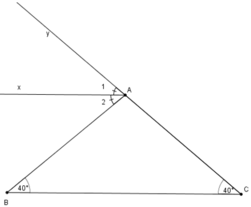
Gọi góc BAy là góc ngoài của tam giác ABC

Mà hai góc này ở vị trí so le trong nên Ax//BC (đpcm).
Đúng 0
Bình luận (0)
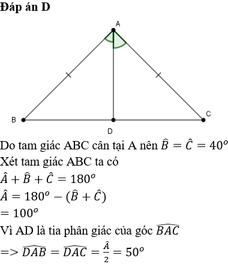
Cho tam giác ABC cân tại A có B = 40 o . Cho AD là tia phân giác của góc BAC. Số đo góc DAB là:
A. 60 °
B. 100 °
C. 30 °
D. 50 °
Tam giác ABC có
∠
A
80
o
,
∠
B
40
o
.
Các đường phân giác BD, CE cắt nhau tại I. Khi đó số đo góc (ACI) là: A.
100
o
B.
80
o
C.
60
o
D.
30
o
Đọc tiếp
Tam giác ABC có ∠ A = 80 o , ∠ B = 40 o . Các đường phân giác BD, CE cắt nhau tại I. Khi đó số đo góc (ACI) là:
A. 100 o
B. 80 o
C. 60 o
D. 30 o
Ta có ∠C = 180o - 80o - 40o = 60o
Vì CI là tia phân giác của góc C nên ∠(ACI) = 60o : 2 = 30o. Chọn D
Đúng 0
Bình luận (0)