x y 20 là cái j

Có 6 cặp số nguyên thỏa mãn điều kiện trên. Đó là:

\(C\text{ặ}p1:1;20\)

Cặp 2:\(2;10\)

Cặp 3:\(4;5\)

Cặp 4:\(-1;-20\)

Cặp 5:\(-2;-10\)

Cặp 6:\(-4;-5\)

Bài này thì chắc k có phương pháp giải

bn có thể liệt kê ra các cặp(x;y) nguyên dương( có 40 cặp) 

còn lại là 40 cặp (x;y) nguyên âm

 Từ đó suy ra có 80 cặp (x;y) nguyên thoả mãn

lớp 7 (,) là giá trị tuyệt đối

co vo so cap so nguyen thoa man

b) Xét \(x=0\)thì \(0+\left|y\right|< 20\)=> \(\left|y\right|< 20\Rightarrow y\in\left\{0;\pm1;\pm2;...;\pm19\right\}\)gồm 39 giá trị

Xét x = \(\pm1\)thì y \(\in\left\{0;\pm1;\pm2;\pm3;...;\pm18\right\}\)gồm 37 giá trị

....

Xét x = \(\pm\)18 thì y \(\in\){0; \(\pm\)1} 

Xét x = \(\pm19\)=> y = 0 , có 1 giá trị

Có tất cả : 2(1 + 3 + ... + 37) + 39 = 761(cặp số)

a; x; y thoả mãn tất cả các giá trị \(|x|\)\(|y|\)\(\le4\)

b, vô số; điều kiện \(|x|+|y|>4\) 

Ta có :\(\left|x\right|\)=\(\orbr{\begin{cases}x\\-x\end{cases}}\)

\(\left|y\right|\)=\(\orbr{\begin{cases}y\\-y\end{cases}}\)

Với x,y ≥0⇒≥0⇒ có 20 cặp .

Với x ≥0 , y<0 => có 20cặp số.

Với x < 0 , y ≥0 => 20 cặp số

Với x <0 , y <0 => có 38 cặp ( Vì loại 1 cặp : |0| + |-20| và | -20| +|0| )

Vậy có 98 cặp x,y thỏa mãn

Ta có: |x|+|y| thì nếu x dương, y dương=> Sẽ có tổng cộng 19x2 = 38 cặp. 

Nếu x,y cùng âm thì cx có tổng cộng 38 cặp.

X dương y âm thì cx có 38 cặp và x âm y dương cx có 38 cặp

=> có tổng cộng 38 . 4 = 152( cặp)

b) Có tổng cộng: 36.4 = 144 cặp

Đáp án D.

Ta có: số proton trung bình là:

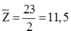
Từ đó ta có thuộc chu kì 1, 2 hoặc 3.

Xét các trường hợp:

Trường hợp 1: X thuộc chu kì 3 =>

Trường hợp 2: X thuộc chu kì 2 =>

=> Y thuộc chu kì 3 hoặc chu kì 4

+ Với Y thuộc chu kì 3 thì ta có

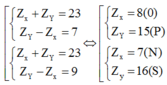
Cả hai kết quả thu được đều thỏa mãn

+ Với Y thuộc chu kì 4 thì ta có

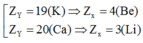
Kết quả thu được cũng thỏa mãn.

- Trường hợp 3: X thuộc chu kì 1:

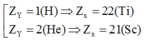
Cả hai kết quả thu được đều không thỏa mãn.

Do đó tất cả có 5 cặp nguyên tố thỏa mãn.