Cho tam giác bác vuông tại a, đường cao h, trung tuyến am.a) chứng minh góc bah=mac.B) Trên đường trung trực Mx của đoạn thẳng bc, Điểm d sao cho md =ma. Chứng Minh rằng ad Là phân giác chung của góc mah và cab
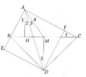
Bài 4. Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM.
a) Chứng minh BAH = MAC.
b) Trên đường trung trực Mx của đoạn thẳng BC, lấy điểm D sao cho MD = MA (D và
A thuộc hai nửa mặt phẳng đối nhau bờ BC). Chứng minh rằng AD là phân giác chung của
МАН & CAB.
c) Từ D kẻ DE, DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì ?
d) Chứng minh ADBE= A
a) Ta có: ^BAH = ^BCA (vì 2 góc này cùng phụ với ^B)
Mà: ^MAC = ^BCA (tg MAC cân tại M vì Tg ABC vuông tại A có AM là trung tuyến)
Nên: ^BAH = ^MAC (4)
b) Tg AMD cân tại M (vì MA=MD) => ^D = ^DAM (1)
Ta có: MD//AH ( vì MD_I_ HM, AH _I_ HM )
Nên: ^D = ^DAH (2)
(1)(2) => ^DAM = ^DAH (3) => AD là p/g của ^HAM (5)
(3)(4) => ^BAH + ^DAH = ^MAC + ^DAM <=> ^BAD=^CAD => AD là p/g của ^BAC (6)
(5)(6) => AD là p/g chung của ^HAM và ^BAC
c) Ta có: AEDF là hcn ( vì ^E=^F=^A=90o )
Mà: AD là p/g của ^EAC (cmt)
Nên: AEDF là hình vuông
d) Tg DBE (^DEA=90o) và tg DCF (^DFC=90o) có:
DE = DF (AEDF là hình vuông)
DB = DC (MD là đường trung trực của BC)
Nên: Tg DBE = tg DCF (ch-cgv)
Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM.
a) Chứng minh B A H ^ = M A C ^ .
b) Trên đường trung trực Mx của đoạn thẳng BC, lấy điểm D sao cho MD = MA (D và A thuộc hai nửa mặt phẳng đối nhau bờ BC). Chứng minh rằng AD là phân giác chung của M A H ^ & C A B ^ .
c) Từ D kẻ DE, DF lần lượt vuông góc với AB và AC. Tứ giác AEDF là hình gì ?
d) Chứng minh Δ D B E = Δ D C F
a) B A H ^ + M A C ^ vì cùng phụ với A B C ^
b) A 1 ^ = C 1 ^ (1) (chứng minh a)
Mà DABC vuông có AM là trung tuyến nên DAMC cân tại M C 1 ^ = A 4 ^ (2).
Từ (1) và (2) suy ra A 1 ^ = A 4 ^ (3)
D thuộc đường trung trực của BC.
Þ DM ^ BC = {M}
Þ D 1 ^ = A 2 ^
Vì DM = MA (giả thiết) ⇒ M 1 ^ = A 3 ^ ⇒ A 2 ^ = A 3 ^ (4)
Từ (3) và (4) Þ AD là phân giác chung của M A H ^ & C A B ^
c) Theo cách vẽ và kết quả câu b), ta có AEDF là hình vuông.
d) DDBE = DDCF (cạnh huyền - cạnh góc vuông)
Cho tam giác vuông tại A, đường cao AH, trưng tuyến AM.
a) So sanh góc BAH và MAC
b) Trên đường trung trực Mx của đoạn thẳng BC, lấy điểm D sao cho MD = MA ( D, A ở hai nửa mặt phẳng khác nhau bờ BC). Chứng minh AD là phân giác chung của các góc MAH và CAB
c) Từ D kẻ DE, DF lần lượt vuông góc với AB, AC. Tứ giác AEDF là hình gì ?
d) Chứng minh tam giác DBE = tam giác DCF
a) Ta có: ^BAH = ^BCA (vì 2 góc này cùng phụ với ^B)
Mà: ^MAC = ^BCA (tg MAC cân tại M vì Tg ABC vuông tại A có AM là trung tuyến)
Nên: ^BAH = ^MAC (4)
b) Tg AMD cân tại M (vì MA=MD) => ^D = ^DAM (1)
Ta có: MD//AH ( vì MD_I_ HM, AH _I_ HM )
Nên: ^D = ^DAH (2)
(1)(2) => ^DAM = ^DAH (3) => AD là p/g của ^HAM (5)
(3)(4) => ^BAH + ^DAH = ^MAC + ^DAM <=> ^BAD=^CAD => AD là p/g của ^BAC (6)
(5)(6) => AD là p/g chung của ^HAM và ^BAC
c) Ta có: AEDF là hcn ( vì ^E=^F=^A=90o )
Mà: AD là p/g của ^EAC (cmt)
Nên: AEDF là hình vuông
d) Tg DBE (^DEA=90o) và tg DCF (^DFC=90o) có:
DE = DF (AEDF là hình vuông)
DB = DC (MD là đường trung trực của BC)
Nên: Tg DBE = tg DCF (ch-cgv)
Cho tam giác abc, đường cao Ah(H thuộc BC)
a) chứng minh:H là trung điểm của BC và góc BAH =góc HAC
b)kẻ HM vuông góc với AB tại M ,HN vuông góc với AC tại N.chứng minh :tam giác AMN cân ở A
c)vẽ điểm P sao cho điểm H là trung điểm của đoạn thẳng NP.chứng minh : đường thẳng BC là đường trung trực của đoạn thẳng MP
Cho tam giác ABC vuông tại A, trên cạnh BC lấy điểm D sao cho BD=BA.Qua D vẽ đường vuông góc với BC cắt AC tại E, cắt BA tại F.
a) Chứng minh tam giác ABE = tam giác DBE
b)Chứng minh BE là đường trung trực của đoạn thẳng AD
c) Chứng minh tam giác BCF cân
d) Gọi H là trung điểm của đoạn thẳng CF. Chứng minh B;E;H thẳng hàng
ma kết gái với dễ thương , còn trai ko phải
Cho tam giác ABC cân tại A có đường cao AH (H thuộc BC)
a) Chứng minh: H là trung điểm BC và hai góc BAH và HAC bằng nhau
b) Kẻ HM vuống góc với AB tại M, HN vuông góc với AC tại N. Chứng minh: tam giác AMN cân tại A
c) Vẽ điểm P sao cho điểm H là trung điểm của đoạn NP. Chứng minh: Đường thẳng BC là trung trực của đoạn MP.
d) MP cắt BC tại điểm K. NK cắt MH tại điểm D. Chứng minh: Ba đường thẳng AH, MN, DP cùng đi qua một điểm
Cm: a) Xét t/giác ABH và t/giác ACH
có AB = AC (gt)
góc AHB = góc AHC = 900 (gt)
AH : chung
=> t/giác ABH = t/giác ACH (ch - cgn)
=> góc BAH = góc HAC (hai góc tương ứng) (Đpcm)
=> BH = CH (hai cạnh tương ứng)
=> H là trung điểm của BC
b) Xét t/giác AMH và t/giác ANH
có góc AMH = góc ANH = 900 (gt)
AH : chung
góc MAH = góc NAH (Cmt)
=> t/giác AMH = t/giác ANH (ch - gn)
=> AM = AN (hai cạnh tương ứng)
=> T/giác AMN là t/giác cân tại A
c) Gọi I là giao điểm của BC và MP
Ta có: T/giác AMH = t/giác ANH (Cmt)
=> MH = HN (hai cạnh tương ứng)
Mà HN = PH (gt)
=> MH = PH
Ta lại có: góc AHM + góc MHB = 900 (phụ nhau)
góc AHN + góc NHC = 900 (phụ nhau)
Và góc AHM = góc AHN (vì t/giác AHM = t/giác AHN)
=> góc MHB = góc NHC
Mà góc NHC = góc BHP
=> góc MHB = góc BHP
Xét t/giác MHI và t/giác PHI
có MH = PH (cmt)
góc MHI = góc IHP (cmt)
HI : chung
=> t/giác MHI = t/giác PHI (c.g.c)
=> MI = PI (hai cạnh tương ứng) => I là trung điểm của MP (1)
=> góc MIH = góc HIP (hai góc tương ứng)
Mà góc MIH + góc HIP = 1800
=> 2.góc MIH = 1800
=> góc MIH = 1800 : 2
=> góc MIH = 900
=> HI \(\perp\)MP (2)
Từ (1) và (2) suy ra HI là đường trung trực của đoạn thẳng MP
hay BC là đường trung trực của đoạc thẳng MP (Đpcm)
d) tự lm
Cm: a) Xét t/giác ABH và t/giác ACH
có AB = AC (gt)
góc AHB = góc AHC = 900 (gt)
AH : chung
=> t/giác ABH = t/giác ACH (ch - cgn)
=> góc BAH = góc HAC (hai góc tương ứng) (Đpcm)
=> BH = CH (hai cạnh tương ứng)
=> H là trung điểm của BC
b) Xét t/giác AMH và t/giác ANH
có góc AMH = góc ANH = 900 (gt)
AH : chung
góc MAH = góc NAH (Cmt)
=> t/giác AMH = t/giác ANH (ch - gn)
=> AM = AN (hai cạnh tương ứng)
=> T/giác AMN là t/giác cân tại A
c) Gọi I là giao điểm của BC và MP
Ta có: T/giác AMH = t/giác ANH (Cmt)
=> MH = HN (hai cạnh tương ứng)
Mà HN = PH (gt)
=> MH = PH
Ta lại có: góc AHM + góc MHB = 900 (phụ nhau)
góc AHN + góc NHC = 900 (phụ nhau)
Và góc AHM = góc AHN (vì t/giác AHM = t/giác AHN)
=> góc MHB = góc NHC
Mà góc NHC = góc BHP
=> góc MHB = góc BHP
Xét t/giác MHI và t/giác PHI
có MH = PH (cmt)
góc MHI = góc IHP (cmt)
HI : chung
=> t/giác MHI = t/giác PHI (c.g.c)
=> MI = PI (hai cạnh tương ứng) => I là trung điểm của MP (1)
=> góc MIH = góc HIP (hai góc tương ứng)
Mà góc MIH + góc HIP = 1800
=> 2.góc MIH = 1800
=> góc MIH = 1800 : 2
=> góc MIH = 900
=> HI ⊥MP (2)
Từ (1) và (2) suy ra HI là đường trung trực của đoạn thẳng MP
hay BC là đường trung trực của đoạc thẳng MP (Đpcm)
1. Cho tam giác ABC vuông tại A. tia phân giác góc B cắt AC tại D. từ A kẻ AE vuông góc BD tại E và cắt BC tại M
A. chứng minh tam giác ABC bằng tam giác MBE
B. chứng minh DM vuông góc với BC
C .Kẻ AH vuông góc với BC tại I. Chứng minh AM là tia phân giác của góc IAC
câu 2: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ tia phân giác AD của góc A (D thuộc BC)
A. chứng minh tam giác ABD bằng tam giác ACD
B. Vẽ đường trung tuyến của tam giác ABC cắt cạnh AC tại G. chứng minh G là trọng tâm của tam giác ABC
C. Gọi H là trung điểm của cạnh DC. qua h Vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh tam giác DEC cân
D. Chứng minh ba điểm B, G, E thẳng hàng
Câu 3 Cho tam giác ABC vuông tại A. Vẽ trung tuyến AM của tam giác ABC, Kẻ MH vuông góc với AC. Trên tia đối của tia MH đặt điểm K sao cho MK bằng MH
a. chứng minh tam giác MHC bằng tam giác MKB và BK vuông góc với KH
B. Chứng minh AB song song với HK và BK = AH.
C. Vẽ BH cắt AB tại g. Gọi I là trung điểm của AB. Chứng minh ba điểm C, G, I thẳng hàng
câu4 Cho tam giác ABC vuông tại A. gọi M là trung điểm cạnh BC. trên tia đối của tia MA lấy điểm D sao cho MD = MA.
A . chứng minh tam giác MCD bằng tam giác MBD và AC song song với BD
B. Gọi I là trung điểm AM, J là trung điểm BM. AJ cắt BI tại G. Chứng minh tam giác GAB là tam giác cân
Câu 5 cho tam giác ABC vuông tại A (AB bé hơn AC). vẽ BD là tia phân giác của góc ABC (D thuộc AC). trên đoạn BC lấy điểm E sao cho BE bằng BA
a chứng minh tam giác ABD bằng tam giác EBD .Từ đó suy ra góc BED là góc vuông
b. tia ED cắt tia BA tại EF. Chứng minh tam giác BED cân
C. Chứng minh tam giác AFC bằng tam giác ECF
D.Chứng minh: AB + AC >DE+BC
câu 6: Cho tam giác ABC vuông tại A. Vẽ đường phân phân giác BD của tam giác ABC và E là hình chiếu của D trên BC
a. chứng minh tam giác ABD bằng tam giác EBD và AE vuông góc với BD
B. Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh tam giác ABC bằng tam giác AFC
C. Qua A vẽ đường thẳng vuông góc với BC cắt CF tại G. Chứng minh ba điểm B, D, G thẳng hàng
câu 7: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ AD là phân giác của góc A (D thuộc BC)
A . Chứng minh tam giác ABD bằng tam giác ACD
B. lấy H là trung điểm của AB. Trên tia đối của tia HC lấy điểm K sao cho HK = HC. Chứng minh rằng AK = BC
c. CH cắt AD tại G. Chứng minh (BA+BC)÷6 >GH
Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).
Cho tam giác ABC vuông tại A , trên cạch BC lấy điểm D sao cho BD = BA. Qua D vẽ đường vuông góc với BC cắt AC tại E, cắt BA tại F.
A. Chứng minh tam giác ABE = tam giác DBE
B. Chứng minh BE là đường trung trực của đoạn thẳng AD C.
C. Chứng minh tam giác BCF cân
D. Gọi H là trung điểm của đoạn thẳng CF . Chứng minh B;E;H thẳng hàng
Tham khảo tại link này nhé !
https://olm.vn/hoi-dap/detail/219404925266.html
a)Xét\(\Delta ABE\)và\(\Delta DBE\)có:
\(AB=DB\left(GT\right)\)
\(\widehat{BAE}=\widehat{BDE}\left(=90^o\right)\)
\(BE\)là cạnh chung
Do đó:\(\Delta ABE=\Delta DBE\)(cạnh huyền-cạnh gv)
b)Vì\(\Delta ABE=\Delta DBE\)(cm câu a) nên\(\widehat{ABE}=\widehat{DBE}\)(2 cạnh t/ứ)
Gọi\(K\)là giao điểm của\(AD\)và\(BE\)
Xét\(\Delta ABK\)và\(\Delta DBK\)có:
\(AB=DB\left(GT\right)\)
\(\widehat{ABK}=\widehat{DBK}\left(cmt\right)\)
\(BK\)là cạnh chung
Do đó:\(\Delta ABK=\Delta DBK\)(c-g-c)
\(\Rightarrow\widehat{AKB}=\widehat{DKB}\)(2 góc t/ứ)
\(AK=DK\)(2 cạnh t/ứ)
Ta có:\(\widehat{AKB}+\widehat{DKB}=180^o\)(2 góc KB)
mà\(\widehat{AKB}=\widehat{DKB}\left(cmt\right)\)
\(\Rightarrow\widehat{AKB}=\widehat{DKB}=\frac{180^o}{2}=90^o\)
\(\Rightarrow BK\perp AD\)
mà \(K\)là trung điểm của\(AD\)do\(AK=DK\left(cmt\right)\)
\(\Rightarrow BK\)là đường trung trực của\(AD\)
c)Xét\(\Delta ABC\)và\(\Delta DBF\)có:
\(\widehat{B}\)là góc chung
\(AB=DB\left(GT\right)\)
\(\widehat{BAC}=\widehat{BDF}\left(=90^o\right)\)
Do đó:\(\Delta ABC=\Delta DBF\)(g-c-g)
\(\Rightarrow BC=BF\)(2 cạnh t/ứ)
Xét\(\Delta BCF\)có:\(BC=BF\left(cmt\right)\)
Do đó:\(\Delta BCF\)cân tại\(A\)(Định nghĩa\(\Delta\)cân)
Cho tam giác ABC vuông tại A và có đường phân giác BD. Kẻ đường thẳng DH vuông góc với BC tại điểm H. Trên tia đối của tia AB lấy điểm K sao cho AK = CH.
1. Chứng minh rằng ∆ABD = ∆HBD.
2. Chứng minh rằng: đường thẳng BD là đường trung trực của đoạn thẳng AH và AD<DC.
3. Chứng minh ba điểm H,D,K thẳng hàng và chứng minh BD vuông góc với KC.
4. (*) Chứng minh rằng 2(AD + AK) > CK.
!Giúp mình với!