cho hình vẽ, ax // by. khi đó a° bằng
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA = a, OB = b (a,b cùng đơn vị: cm).
Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).
Tính diện tích hình thang ABCD khi C O A ^ = 60 o
Cho đồ thị hàm số y = ax (a ≠ 0) là đường thẳng OM trên hình vẽ. Khi đó hệ số a bằng
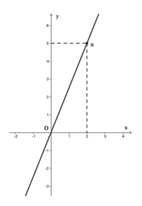
A. 5
B. 5/2
C. 2/5
D. 1
Từ đồ thị hàm số ta thấy điểm M(2, 5) thuộc đồ thị hàm số nên ta thay x = 2, y = 5 vào hàm số y = ax (a ≠ 0) ta được 5 = a.2 ⇒ a = 5/2 (TM)
Vậy a = 5/2
Chọn đáp án B
Cho đồ thị hàm số y = ax (a ≠ 0) là đường thẳng OM trên hình vẽ. Khi đó hệ số a bằng
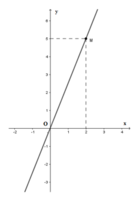
A. 5
B. 5/2
C. 2/5
D. 1
Từ đồ thị hàm số ta thấy điểm M(2, 5) thuộc đồ thị hàm số nên ta thay x = 2; y = 5 vào hàm số y = ax (a ≠ 0) ta được 5 = a.2 ⇒ a = 5/2 (TM)
Vậy a = 5/2
Chọn đáp án B
Cho đồ thị hàm số y = ax ( a ≠ 0 ) là đường thẳng OM trên hình vẽ . Khi đó hệ số a bằng
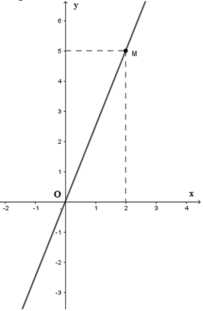
A. 5
B. 5 2
C. 2 5
D. 1
Từ đồ thị hàm số ta thấy điểm M(2;5)thuộc đồ thị hàm số nên ta thay x = 2; y = 5 vào hàm số y = ax ( a ≠ 0 ), được: 5= a.2 => a = 5 2 (TM)
Vậy a = 5 2
Đáp án cần chọn là: B
Cho đồ thị hàm số y = ax ( a ≠ 0 ) là đường thẳng OB trên hình vẽ . Khi đó hệ số a bằng

A. − 1 2
B. -2
C. 1 2
D. 2
Từ đồ thị hàm số ta thấy điểm B(1;-2) thuộc đồ thị hàm sốy = ax ( a ≠ 0 ) nên ta thay x = 1; t = -2 vào hàm số y = ax ta được: -2 = a.1 => a = -2(thỏa mãn)
Vậy a = -2.
Đáp án cần chọn là: B
Cho hình vẽ bên, biết Ax//By, góc A bằng 20o, góc B bằng 120o. Tính số đo x (góc C)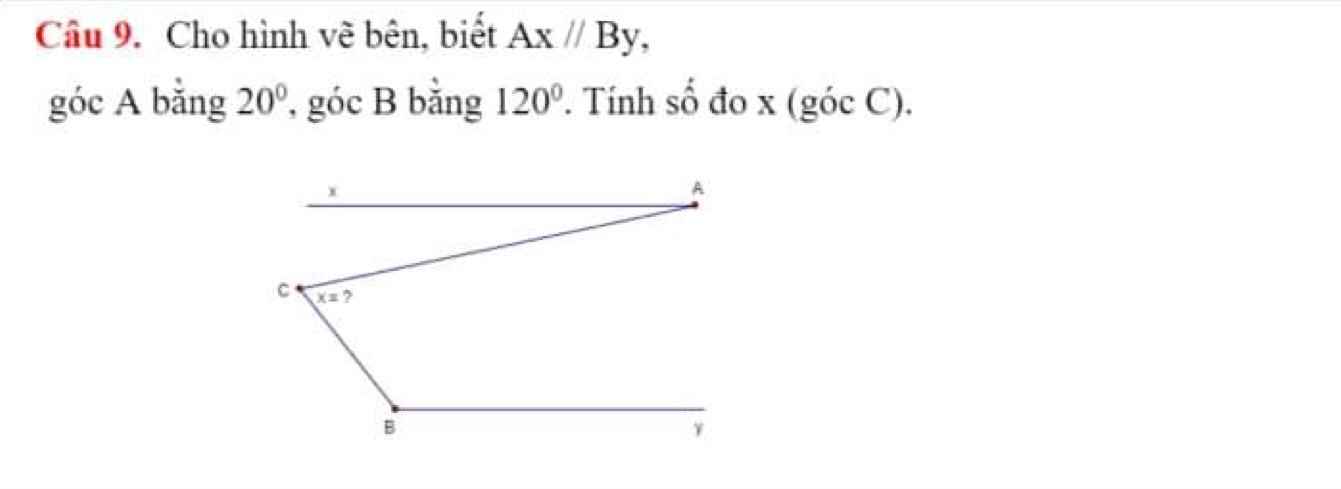
Cho ba điểm A, O, B thẳng hàng, OA = a, OB = b (a, b cùng đơn vị là cm). Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D
a, Chứng minh các tam giác AOC và BDO đồng dạng. Từ đó suy ra tích AC.BD không đổi
b, Với C O A ^ = 60 0 , hãy:
i, Tính diện tích hình thang ABCD
ii, Tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành khi cho hình vẽ quay xung quanh AB
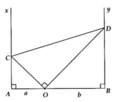
a, A O C ^ = O D B ^ (cùng phụ B O D ^ )
=> DAOC ~ DBDO (g.g)
=> A C B O = A O B D
=> AC.BD = a.b (không đổi)
b, Ta có C O A ^ = O D B ^ = 60 0 , A C O ^ = D O B ^ = 30 0 , AC = a 3 , BD = b 3 3
i, S A B C D = 3 a + b 3 a + b 6
ii, 9
Cho ba điểm A, O, B thẳng hàng theo thứ tự đó, OA = a, OB = b (a,b cùng đơn vị: cm).
Qua A và B vẽ theo thứ tự các tia Ax và By cùng vuông góc với AB và cùng phía với AB. Qua O vẽ hai tia vuông góc với nhau và cắt Ax ở C, By ở D (xem hình 116).
a) Chứng minh AOC và BDO là hai tam giác đồng dạng; từ đó suy ra tích AC.BD không đổi.
b) Tính diện tích hình thang ABCD khi COA ^ = 60 °
c) Với COA ^ = 60 ° cho hình vẽ quay xung quanh AB. Tính tỉ số thể tích các hình do các tam giác AOC và BOD tạo thành.
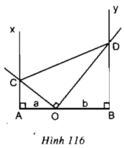


c) Khi quay hình vẽ xung quanh cạnh AB: ΔAOC tạo nên hình nón, bán kính đáy là AC, chiều cao AO; ΔBOD tạo nên hình nón, bán kính đáy BD, chiều cao OB.

Vẽ cặp góc so le trong x A B ⏜ v à y B A ⏜ và có số đo đều bằng 120°. Khi đó Ax và By:
A. Song song
B. Cắt nhau
C. Trùng nhau
D. Vuông góc
Ta có hình vẽ như sau:
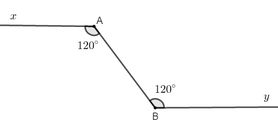
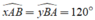
Mà hai góc này ở vị trí so le trong
Do đó Ax // By
Chọn đáp án A