Trên mặt phẳng tọa độ, tìm tập hợp biểu diễn của các số phức z thỏa mãn điều kiện: |z|≤2

Những câu hỏi liên quan
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: |2 + z| < |2 – z|
Ta có: | 2 + z | 2 < | 2 - z | 2
⇔ | 2 + x + iy | 2 < | 2 - x - iy | 2
⇔ 2 + x 2 + y 2 < 2 - x 2 + - y 2
⇔ x < 0
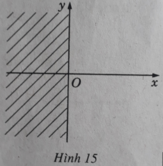
Đó là tập hợp các số phức có phần thực nhỏ hơn 0, tức là nửa trái của mặt phẳng tọa độ không kể trục Oy.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ, tìm tập hợp biểu diễn của các số phức z thỏa mãn điều kiện: Phần ảo của z bằng -2
Phần ảo của z bằng -2
⇔ y = -2
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng y = -2.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| 10. A. Đường tròn ( x - 2) 2 + ( y + 2) 2 100. B. Elip C. Đường tròn ( x -2) 2 + ( y + 2) 2 10. D. Elip
Đọc tiếp
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10.
A. Đường tròn ( x - 2) 2 + ( y + 2) 2 = 100.
B. Elip 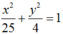
C. Đường tròn ( x -2) 2 + ( y + 2) 2 = 10.
D. Elip 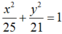
Chọn D.
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi, x, y ∈ R
Gọi A là điểm biểu diễn số phức 2
Gọi B là điểm biểu diễn số phức -2
Ta có: |z – 2| + |z + 2| = 10 ⇔ MB + MA = 10.
Ta có AB = 4.
Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A(2; 0), B( -2; 0) tiêu cự AB = 4 = 2c, độ dài trục lớn là 10 = 2a , độ dài trục bé là ![]()
Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10 là elip có phương trình 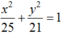
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện: 1<|z| ≤ 2
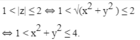
Vậy tập hợp điểm M là hình vành khăn tâm O, bán kính đường tròn nhỏ bằng 1,đường tròn lớn bằng 2, không kể các điểm thuộc đường tròn nhỏ.
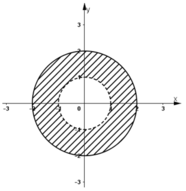
Đúng 0
Bình luận (0)
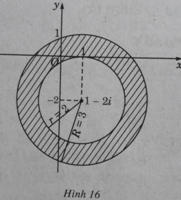
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: 2 ≤ |z − 1 + 2i| < 3
Đó là những điểm nằm phía trong hình tròn bán kính bằng 3 và phía ngoài (kể cả biên) hình tròn bán kính bằng 2 có cùng tâm là điểm biểu diễn số phức z 0 = 1 – 2i , tức là những điểm nằm trong hình vành khăn kể cả biên trong. Đó là những điểm (x; y) trên mặt phẳng tọa độ thỏa mãn điều kiện: 4 ≤ x - 1 2 + y + 2 2 < 9
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ, tìm tập hợp biểu diễn của các số phức z thỏa mãn điều kiện: Phần thực của z bằng 1
Điểm M(x; y) biểu diễn số phức z = x + yi.
Phần thực của z bằng 1
⇔ x = 1
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng x = 1.
Đúng 0
Bình luận (0)
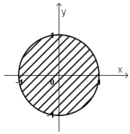
Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện: |z| ≤ 1
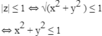
Vậy tập hợp điểm M là hình tròn tâm O(0; 0), bán kính R = 1.
Đúng 0
Bình luận (0)
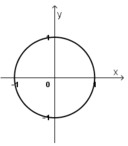
Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện: |z| = 1
Gọi số phức z = x + y.i có điểm biểu diễn là M(x; y).
|z| = 1 ⇔ x 2 + y 2 = 1 ⇔ x 2 + y 2 =1
Vậy tập hợp điểm M là đường tròn tâm O(0; 0), bán kính R = 1.
Đúng 0
Bình luận (0)
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: |z – i| = 1
Vế trái là khoảng cách từ điểm biểu diễn z dến điểm biểu diễn z 0 = 0 + i . Vậy tập hợp các điểm thỏa mãn điều kiện đã cho là tất cả các điểm cách điểm (0; 1) một khoảng không đổi bằng 1. Đó là các điểm nằm trên đường tròn bán kính bằng 1 và tâm là điểm (0; 1) (H. 14)
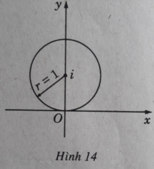
Ta có thể tiến hành như sau:
Cho z = x + iy, ta có | z - 1 | 2 = | x + y - 1 i | 2 = x 2 + y - 1 2 và như vậy ta có: x 2 + y - 1 2 = 1
Đây là phương trình đường tròn bán kính bằng 1 và tâm là (0; 1)
Đúng 0
Bình luận (0)


