Các bạn giúp mình với ạ !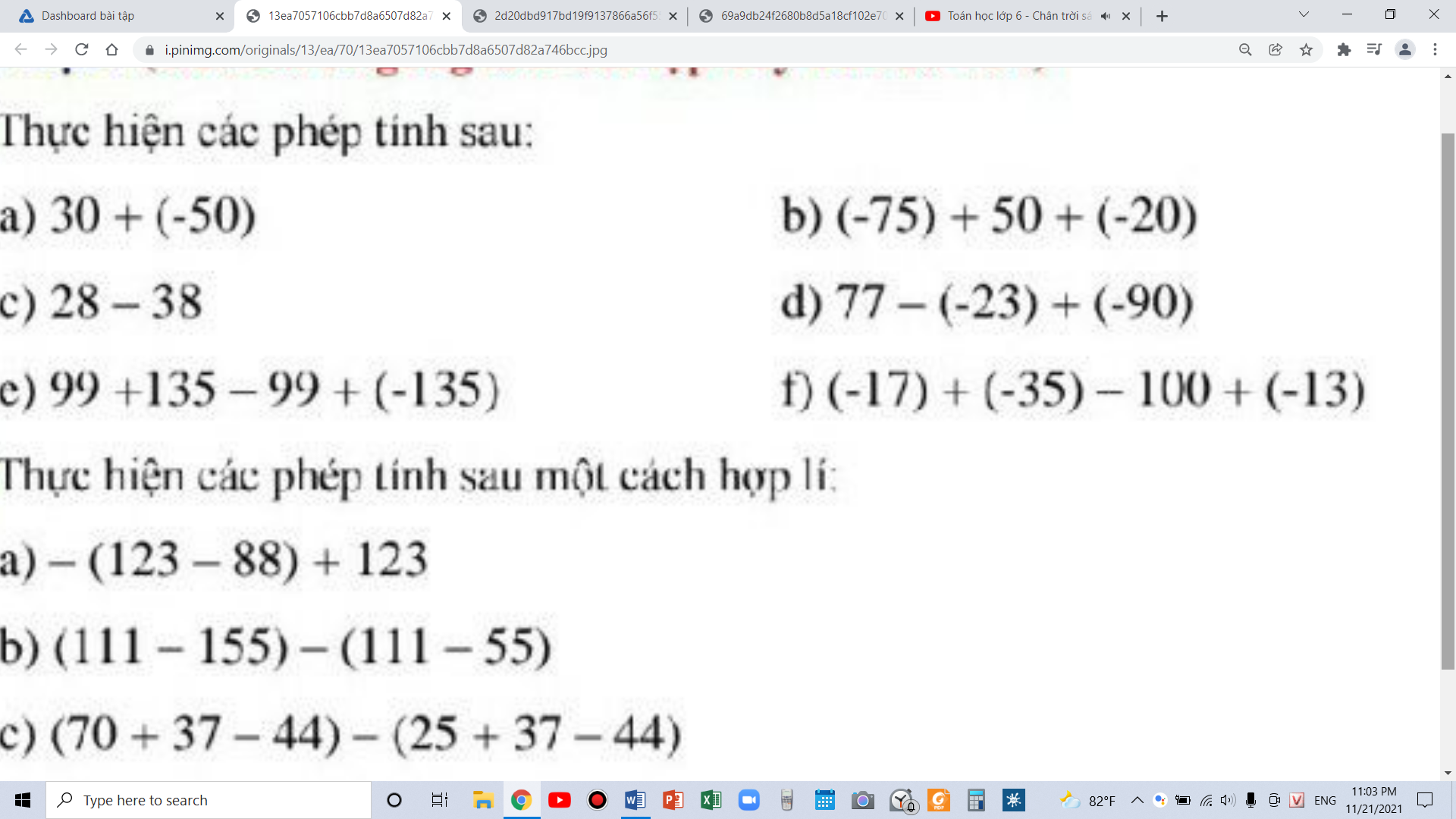

Những câu hỏi liên quan
Các bạn giúp mình với ạ😓😓
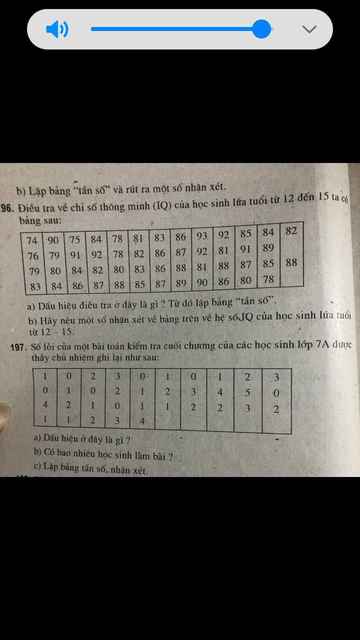
Giúp mình với. Mình đang cần gấp ạ😓😓😓

27.
Bán kính mặt cầu ngoại tiếp tứ diện vuông được tính bằng:
\(R=\sqrt{\dfrac{OA^2+OB^2+OC^2}{4}}=\sqrt{\dfrac{1^2+2^2+3^2}{4}}=\dfrac{\sqrt{14}}{2}\)
28.
Từ giả thiết suy ra \(A\left(2;2;2\right)\)
Gọi điểm thuộc mặt Oxz có tọa độ dạng \(D\left(x;0;z\right)\)
\(\Rightarrow\overrightarrow{AD}=\left(x-2;-2;z-2\right)\)
\(\overrightarrow{BD}=\left(x+2;-2;z\right)\) ; \(\overrightarrow{CD}=\left(x-4;-1;z+1\right)\)
D cách đều A, B, C \(\Rightarrow\left\{{}\begin{matrix}AD=BD\\AD=CD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x+2\right)^2+4+z^2\\\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x-4\right)^2+1+\left(z+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+z=1\\2x-3z=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}z=-\dfrac{1}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow P\left(\dfrac{3}{4};0;-\dfrac{1}{2}\right)\)
Đúng 1
Bình luận (0)
29.
Do tâm I mặt cầu thuộc Oz nên tọa độ có dạng: \(I\left(0;0;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AI}=\left(-3;1;z-2\right)\\\overrightarrow{BI}=\left(-1;-1;z+2\right)\end{matrix}\right.\)
Mặt cầu qua A, B nên \(AI=BI\)
\(\Leftrightarrow3^2+1^2+\left(z-2\right)^2=1^2+1^2+\left(z+2\right)^2\)
\(\Leftrightarrow8z=8\Rightarrow z=1\)
\(\Rightarrow I\left(0;0;1\right)\Rightarrow R=IB=\sqrt{1^2+1^1+3^2}=\sqrt{11}\)
Phương trình mặt cầu:
\(x^2+y^2+\left(z-1\right)^2=11\)
Đúng 1
Bình luận (0)
30.
Từ phương trình mặt cầu ta có:
\(R=\sqrt{1^2+\left(-2\right)^2+2^2-\left(-m\right)}=\sqrt{m+9}\)
\(\Rightarrow\sqrt{m+9}=5\Rightarrow m=16\)
31.
Khoảng cách giữa điểm M và điểm đối xứng với nó qua Ox là \(2\sqrt{y_M^2+z_M^2}=2\sqrt{65}\)
32.
Gọi \(I\left(x;y;z\right)\) là tâm mặt cầu
\(\overrightarrow{AI}=\left(x-1;y;z\right)\) ; \(\overrightarrow{BI}=\left(x;y-1;z\right)\) ; \(\overrightarrow{CI}=\left(x;y;z+1\right)\); \(\overrightarrow{DI}=\left(x-1;y;z-3\right)\)
Do I là tâm mặt cầu
\(\Rightarrow\left\{{}\begin{matrix}AI=BI\\AI=CI\\AI=DI\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(x-1\right)^2+y^2+z^2=x^2+\left(y-1\right)^2+z^2\\\left(x-1\right)^2+y^2+z^2=x^2+y^2+\left(z-1\right)^2\\\left(x-1\right)^2+y^2+z^2=\left(x-1\right)^2+y^2+\left(z-3\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-x+y=0\\-x+z=0\\-6z+9=0\end{matrix}\right.\) \(\Rightarrow x=y=z=\dfrac{3}{2}\)
Hay \(I\left(\dfrac{3}{2};\dfrac{3}{2};\dfrac{3}{2}\right)\) \(\Rightarrow D\) đúng
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp mình câu 3 với ạ. Cần gấp 😓😓😓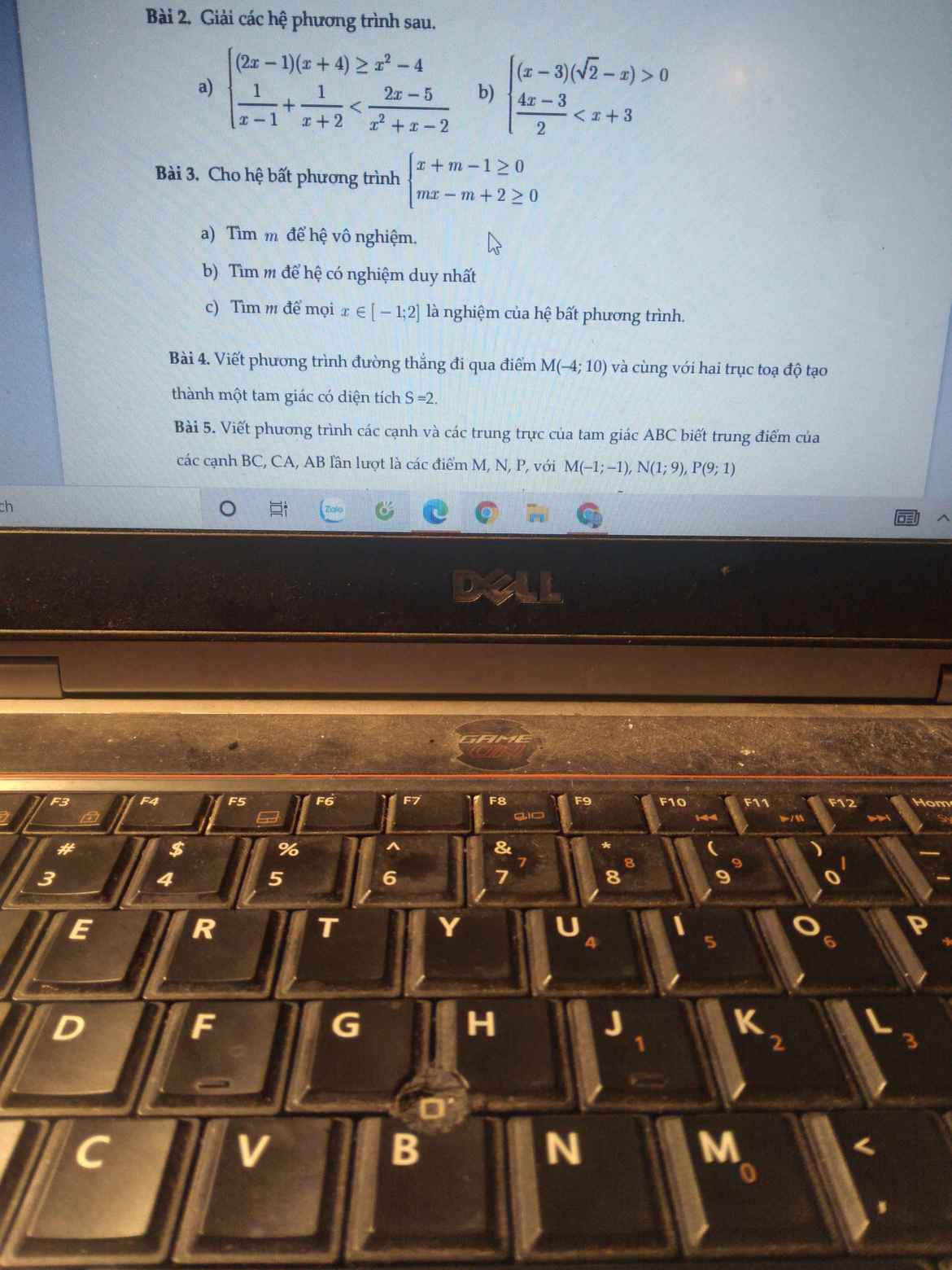
C3: Hệ bpt trở thành: \(\left\{{}\begin{matrix}x\ge1-m\\mx\ge2-m\end{matrix}\right.\)
a, Để hệ phương trình vô nghiệm thì \(m=0\)
b, Để hệ có nghiệm duy nhất thì \(\left\{{}\begin{matrix}m\ne0\\\dfrac{m-2}{m}=1-m\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}m\ne0\\m=\pm\sqrt{2}\end{matrix}\right.\) \(\Leftrightarrow\) \(m=\pm\sqrt{2}\)
c, \(x\in\left[-1;2\right]\) \(\Leftrightarrow\) \(-1\le x\le2\)
Để mọi \(x\in\left[-1;2\right]\) là nghiệm của hệ bpt trên thì
\(\left\{{}\begin{matrix}-1\le1-m\le2\\-1\le\dfrac{2-m}{m}\le2\end{matrix}\right.\) với \(m\ne0\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}2\ge m\ge-1\\m\ge\dfrac{2}{3}\end{matrix}\right.\) \(\left(m\ne0\right)\)
\(\Leftrightarrow\) \(2\ge m\ge\dfrac{2}{3}\)
Vậy \(m\in\left[\dfrac{2}{3};2\right]\) thì mọi \(x\in\left[-1;2\right]\) là nghiệm của hệ bpt
Chúc bn học tốt!
Đúng 2
Bình luận (0)
Giúp mình câu c bài 2 với ạ 😣😓😓😓
Quả trứng có trước hay con gà có trước, giúp mình với ạ 😓😓😓😓😥😥
Quả trứng có trước hay còn gà có trước ý
Goole mà tra
gà có trước thì mới đẻ được trứng
Có gà thì mới có trứng có trứng thì cũng mới có gà
Thì cho quả trứng có trước
Xem thêm câu trả lời
Giúp em câu b bài 1 với ạ😓😓😓😓😓😓
Phương trình hoành độ giao điểm (d) và (P):
\(x^2-2x-3=ax-a-3\)
\(\Leftrightarrow x^2-\left(a+2\right)x+a=0\)
\(\Delta=\left(a+2\right)^2-4a=a^2+4>0;\forall a\Rightarrow\) (d) luôn cắt (P) tại 2 điểm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=a+2\\x_Ax_B=a\end{matrix}\right.\)
Mặt khác do A, B thuộc (d) nên: \(\left\{{}\begin{matrix}y_A=ax_A-a-3\\y_B=ax_B-a-3\end{matrix}\right.\)
\(y_A+y_B=0\)
\(\Leftrightarrow a\left(x_A+x_B\right)-2a-6=0\)
\(\Leftrightarrow a\left(a+2\right)-2a-6=0\)
\(\Leftrightarrow a^2-6=0\)
\(\Leftrightarrow a=\pm\sqrt{6}\)
Đúng 0
Bình luận (0)
Giúp mk câu 16,17 ,18 với ạ 😓😓😓😓😓😞
Câu 16.
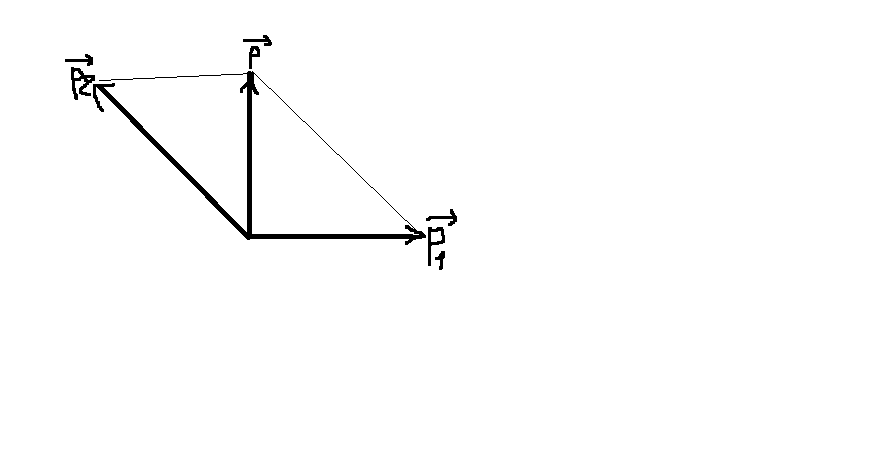
Hình vẽ tương đối thôi nha!!!
Bảo toàn động lương ta có:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
\(\Rightarrow p^2=p_2^2-p_1^2\)\(\Rightarrow p_2=\sqrt{p^2+p_1^2}\)
\(\Rightarrow m_2\cdot v_2=\sqrt{\left(m_1+m_2\right)\cdot v+m_1\cdot v_1}\)
\(\Rightarrow0,3\cdot v_2=\sqrt{[\left(0,5+0,3\right)\cdot3]^2+(0,5\cdot4)^2}=3,124\)
\(\Rightarrow v_2=10,41\)m/s
Đúng 3
Bình luận (0)
Giúp mình với mn ơi 😓😓😓 nếu đc có thể ghi giúp mình tự chọn là từ loại j với 😓😓😓
1A(adj)
2D(n)
3A(adj)
4C(n)
5D(adj)
6C(adj)
7B(n)(Tham khảo c7)
8A(n)
9C(n)
10B(v)
11A(adv)
Đúng 2
Bình luận (2)
Giúp mình với mn ơi 😓😓😓

Giúp mình với mn ơi 😓😓😓














