Cho góc x O y ^ = 45 ∘ . Trên nửa mặt phẳng bờ Ox không chứa tia Oy vẽ x O z ^ = 70 ∘ . Trong ba tia O x , O y , O t tia nào nằm giữa hai tia còn lại? Vì sao?
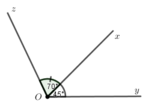
trên đường thẳng xx' lấy 1 điểm O . Trên nửa mặt phẳng bờ xx' vẽ tia Oy sao cho góc xOy = 45 độ . Trên nửa mặt phẳng bờ kia vẽ tia Oz sao cho Oz ⊥ Ox . Gọi Oy' là tia phân giác của góc x'Oz
a) chứng minh góc xOy và x'Oy' là 2 góc đối đỉnh
b) trên nửa mặt phẳng bờ xx' có chứa tia Oy vẽ tia Ot sao cho Ot ⊥Oy . Hãy tính góc x' Ot
Cho góc x O y ^ = 45 ∘ . Trên nửa mặt phẳng bờ Ox không chứa tia Oy vẽ x O z ^ = 70 ∘ . Tính số đo góc yOz.
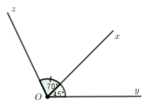
Vì tia Ox nằm giữa hai tia Ozvà Oy nên
x O z ^ + x O y ^ = z O y ^ 70 ∘ + 45 ∘ = z O y ^ z O y ^ = 115 ∘
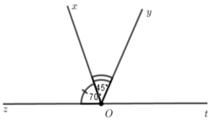
Trên đoạn thẳng AM lấy điểm O trên cùng một nửa mặt phẳng bờ AM vẽ tia OB,OC sao cho góc MOC=115 độ,góc BOC=70 độ trên nửa mặt phẳng đối diện tia OD(D không cùng nằm trên nửa mặt phẳng với BC)bờ AM sao cho góc AOD=45 độ
Cho góc xOy khác góc bẹt, trên nửa mặt phẳng bờ chứa tia Ox không chức tia Oy. Vẽ Oy' vuông góc vs tia Oy. Trên nửa mặt phẳng bờ chứa tia Oy , không chứa tia Ox. Vẽ tia Ox' sao cho Ox' vuông góc vs tia Ox. So sánh góc xOy' và góc x'Oy
Trên đường thẳng xx' lấy điểm O. Trên nửa mặt phẳng bờ xx’, vẽ tia Oy sao cho x O y ^ = 45 ° , Trên nửa mặt phẳng còn lại, vẽ tia Oz sao cho O z ⊥ O x . Gọi Oy' là phân giác của x ' O z ^
a) Chứng minh x O y ^ và x ' O y ' ^ là hai góc đối đỉnh.
b) Trên nửa mặt phẳng bờ xx' chứa tia Oy, vẽ tia Ot sao cho Ot vuông góc với Oy. Hãy tính x ' O t ^
Trên đường thẳng xx' lấy điểm O. Trên nửa mặt phẳng bờ xx’, vẽ tia Oy sao cho x O y ^ = 45°, Trên nửa mặt phẳng còn lại, vẽ tia Oz sao cho Oz ⊥ Ox. Gọi Oy' là phân giác của x ' O z ^
a) Chứng minh x O y ^ và x ' O y ' ^ là hai góc đối đỉnh.
b) Trên nửa mặt phẳng bờ xx' chứa tia Oy, vẽ tia Ot sao cho Ot vuông góc với Oy. Hãy tính x ' O t ^
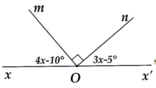
a) Vì Oy' là phân giác x ' O z ^ nên
x ' O y ' ^ = 1 2 x ' O z ^ = 1 2 . 90° = 45°
=> x O y ^ = x ' O y ' ^
Mà Ox và Ox' là hai tia đối nhau nên
x O y ^ và x ' O y ' ^ đối đỉnh
b) x ' O y ^ = 45°, y ' O t ^ = 90° => Ox' là phân giác t O y ' ^
Do đó x ' O t ^ = 45°
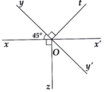
Trên đường thẳng xx' lấy điểm O. Trên nửa mặt phẳng bờ xx' vẽ Oy sao cho góc xOy = 45 độ .Trên nửa mặt phẳng đối vẽ tia Oz vuông góc với tia Ox tại O. Gọi Oy' là tia phân giác của góc x'Oz.
a,Chứng minh góc xOy và góc x'Ot là hai góc đối đỉnh.
b,Trên nửa mặt phẳng bờ xx' có chứa tia Oy, vẽ tia Ot vuông góc với Oy tại O. Hãy tính góc x'Ot.
a) (Sửa lại là xOy và x'Oy' đối đỉnh nha, k có t trog đề bài ![]() )
)
Ta có : \(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-45^o=135^o\)
Oy là tia phân giác của góc x'Oy' nên \(\widehat{x'Oy'}=\frac{1}{2}\widehat{x'Oz}=\frac{1}{2}.90^o=45^o\)
Do đó \(\widehat{x'Oy}+\widehat{x'Oy'}=135^o+45^o=180^o\) => Oy, Oy' là 2 tia đối nhau (1)
; đã có điểm O trên đg thẳng xx' nên Ox, Ox' đối nhau (2)
Từ (1) và (2) => góc xOy và x'Oy' đối đỉnh
b) Ta có : \(\widehat{xOy}+\widehat{yOt}+\widehat{x'Ot}=180^o\) (kề bù)
=> \(\widehat{x'Ot}=180^o-45^o-90^o=45^o\)
Trên đoạn thẳng AM lấy O. Trên cùng một nửa mặt phẳng bờ AM vẽ các tia OB,OC sao cho góc MOC = 100 ; góc BOC = 70 . Trên nửa mặt phẳng đối diện dựng tia OC ( D không cùng nằm trên nửa mặt phẳng với BC bờ AM sao cho góc AOD = 45 a) Tính góc MOB và góc AOB b) Chứng tỏ 3 điểm D,O,B thẳng hàng
Cho góc x O y ^ = 45 ∘ . Trên nửa mặt phẳng bờ Ox không chứa tia Oy vẽ x O z ^ = 70 ∘ . Vẽ Ot là tia đối của tia Oz Tính số đo góc x O t ^ .
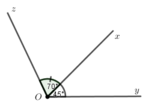
Vì z O x ^ và z O x ^ là hai góc kề bù nên
z O x ^ + x O t ^ = 180 ∘ 70 ∘ + x O t ^ = 180 ∘ x O t ^ = 180 ∘ − 70 ∘ x O t ^ = 110 ∘
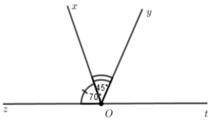
Trên đường thẳng xx' lấy điểm O. Trên nửa mặt phẳng bờ xx', vẽ tia Oy sao cho góc xOy = 45o. Trên nửa mặt phẳng còn lại, vẽ tia Oz sao cho Oz_I_ Ox. Gọi Oy' là phân giác của góc x'Oz
a) Chứng minh góc xOy và góc x'Oy' là 2 góc đối đỉnh
b) Trên nửa mặt phẳng bờ xx' chứa tia Oy, vẽ tia Ot sao cho Ot vuông góc với Oy. Tính góc x'Ot
a) Ox' và Ox là hai tia đối nhau nên
\(\widehat{xOx'}=180^o\)mà \(\widehat{xOz}=90^o\)
\(\Rightarrow\widehat{x'Oz}=90^o\)
Mặt khác Oy' là tia phân giác của \(\widehat{x'Oz}\)
nên \(\widehat{x'Oy'}=\widehat{zOy'}=\frac{1}{2}\cdot90^o=45^o\)
\(\Rightarrow\widehat{x'Oy'}=\widehat{xOy}=45^o\)
Mà Ox' và Ox là 2 tia đối nhau, 2 tia Oy' và Oy thuộc 2 mặt phẳng đối nhau bờ là xx'
Do đó \(\widehat{x'Oy'}\)và \(\widehat{xOy}\)là 2 góc đối đỉnh. ( đpcm )
b) Ta có: Oy' và Oy là 2 tia đối nhau ( cmt )
\(\Rightarrow\widehat{yOt}+\widehat{tOy'}=180^o\)
\(\Rightarrow90^o+\widehat{tOy'}=180^o\)
\(\Rightarrow\widehat{tOy'}=90^o\)
Lại có Oy' và Oy thuộc 2 nửa mặt phẳng đối nhau bờ là xx' nên Ox' nằm giữa 2 tia Oy và Oy'
\(\Rightarrow\widehat{x'Ot}+\widehat{x'Oy'}=\widehat{tOy'}\)
\(\Rightarrow\widehat{x'Ot}+45^o=90^o\)
\(\Rightarrow\widehat{x'Ot}=45^o\)
Vậy \(\widehat{x'Ot}=45^o\)