Cho các hàm số
y
x
α
,
y
x
β
,
y
x
γ
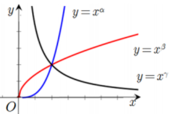
có đồ thị trên cùng một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào dưới đây đúng
Đọc tiếp
Cho các hàm số y = x α , y = x β , y = x γ có đồ thị trên cùng một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào dưới đây đúng
![]()
![]()
![]()
![]()
