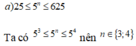Tìm số nguyên dương n, biết: 25< 5n < 625;

Những câu hỏi liên quan
Tìm số nguyên dương n biết: 25 ≤ 5 n ≤ 625
Bài 6A : Tìm số nguyên dương n biết :
a)25 < 5n < 625
Ta có:\(25< 5^n< 625\)
\(\Leftrightarrow5^2< 5^n< 5^4\)
\(\Leftrightarrow2< x< 4\)
\(\Leftrightarrow x=3\)
Vậy \(x=3\)
Đúng 0
Bình luận (0)
25 < 5n < 625
=> 52 < 5n < 54
=> 2 < n < 4
=> n = 3
Đúng 0
Bình luận (0)
25 < 5n < 625
52 < 5n < 54
\(\Rightarrow\)2 < n < 4
\(\Rightarrow\)n = 3
Đúng 0
Bình luận (0)
Tìm số nguyên dương n biết:
25 < 5^n < 625
Giups nha mình tick cho
25 < 5n < 625
52 < 5n < 54
\(\Rightarrow\)2 < n < 4
\(\Rightarrow\)n = 3
tìm số nguyên dương n, biết:
a) 25<5n<625
b)3.27>3nlớn hơn, bằng 9
c)16 bé hơn, bằng 8n bé hơn, bằng 64
a) \(25< 5^n< 625\)
\(25=5^2;625=5^4\)
=> \(5^2< 5^n< 5^4\)
=> 2 < n < 4
=> n = 3
b) \(9\le3^n< 3.27\)
\(9=3^2;3.27=3.3^3=3^4\)
=> \(3^2\le3^n< 3^4\)
=> n = 2; hoặc n = 3
c) \(16\le8^n\le64\)
\(16=8.2;64=8^2\)
=> \(8.2\le8^n\le8^2\)
=> n = 2
Tìm số tự nhiên n biết :
a.3n= 27
b. 5n= 625
`@` `\text {Ans}`
`\downarrow`
`a.`
`3^n = 27` phải k c?
`3^n = 27`
`=> 3^n = 3^3`
`=> n=3`
Vậy, `n=3`
TH2 (đề):
`3n = 27`
`=> n = 27 \div 3`
`=> n=9`
Vậy, `n=9`
`b.`
TH1:
`5^n = 625`
`=> 5^n = 5^4`
`=> n = 4`
Vậy, `n=4`
TH2:
`5n = 625`
`=> n = 625 \div 5`
`=> n = 125`
Vậy, `n=125`
Đúng 3
Bình luận (0)
1. Cho a,b,c nguyên dương sao cho (a-b)(a-c)(b-c)=a+b+c. Tìm GTNN M=a+b+c
2. Tìm n nguyên để \(A=\sqrt{\frac{25}{2}+\sqrt{\frac{625}{4}-n}}+\sqrt{\frac{25}{2}-\sqrt{\frac{625}{4}-n}}\)là số nguyên
3. Cho a,b,c dương. CMR \(\frac{a^3b}{3a+b}+..\)(hoán vị) \(\ge hoánvị\frac{a^2bc}{2a+b+c}\)
2. ĐK: \(0\le x\le\frac{625}{4}\)
Đặt \(x=\sqrt{\frac{25}{2}+\sqrt{\frac{625}{4}-n}}+\sqrt{\frac{25}{2}-\sqrt{\frac{625}{4}-n}}\)
Ta tính được \(x^2=25+2\sqrt{n}\le25+2.\frac{25}{2}=50\)
Hiển nhiên \(x^2\ge25\) và là số chính phương nên \(x^2=25+2\sqrt{n}\) nhận các giá trị 25; 36; 49
Tìm được n = 0 và n = 144
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
252. (5n)2=625
Tìm n
25^2.(5n)^2=625
=> 625.(5n)^2=625
=>(5n)^2=625:625=1
=>(5n)^2=1=>5n=1(vì 1^2=1)
=>n=0,2 ( hoặc 1/5)
Đúng 0
Bình luận (0)
tìm số nguyên dương n nhỏ nhất sao cho n^2+5n+1 là số nguyên tố
tìm số nguyên dương n nhỏ nhất sao cho n^2 + 5n+ 1 là số nguyên tố
n=1
vì 12 + 5.1+1 =1+5+1=7 (thỏa mãn vì 7 là số nguyên tố)
Vậy n = 1
Đúng 0
Bình luận (0)
ta có
n^2 + 5n + 1
= n ( n+5) + 1
vì 1 là số nguyên tố nên n^2 + 5n + 1 là số nguyên tố
thì n( n+5) là số nguyên tố
=> n (n+5) chia hết cho 1 và n( n+5)
=> .........
Đúng 0
Bình luận (0)