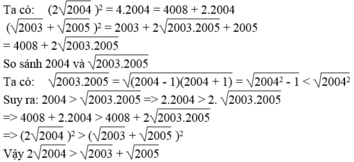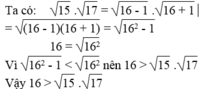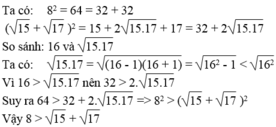Đặt A = \(\sqrt{2003}+\sqrt{2005}\)

B = \(2\sqrt{2004}\)

\(\Rightarrow A^2=2003+2005+2\sqrt{\left(2003.2005\right)}=4008+2\sqrt{\left(2004-1\right)\left(2004+1\right)}\)

\(=4008+2\sqrt{\left(2004^2-1\right)}\)

\(\Rightarrow B^2=4.2004=2.2004+2.2004=4008+2\sqrt{2004^2}\)

mà \(\sqrt{2004^2>\sqrt{ }2004^2-1}\)

\(\Rightarrow B^2>A^2\Rightarrow B>A\Rightarrow2\sqrt{2004}>\sqrt{2003}+\sqrt{2005}\)

Nhớ k cho mình nhé! Thank you!!!

cần lắm một người nào đó giúp mình,hạn chót là ngày mai rồi

Ta có

\(\sqrt{2005}-\sqrt{2004}=\dfrac{1}{\sqrt{2005}+\sqrt{2004}}\)

và \(\sqrt{2004}-\sqrt{2003}=\dfrac{1}{\sqrt{2004+\sqrt{2003}}}\)

Quy về so sánh

\(\dfrac{1}{\sqrt{2005}+\sqrt{2004}}\) với \(\dfrac{1}{\sqrt{2004}+\sqrt{2003}}\)

Khi đó ,ta thấy ngay ở biểu thức thứ nhất lớn hơn mẫu ở biểu thức thứ hai ,các số này đều dương nên suy ra

\(\sqrt{2005}-\sqrt{2004}< \sqrt{2004}-\sqrt{2003}\)

Đặt A = \(\sqrt{ }\)2003 + \(\sqrt{ }\)2005 ; B = 2\(\sqrt{ }\)2004
A² = 2003 + 2005 + 2\(\sqrt{ }\)(2003.2005)
= 4008 + 2\(\sqrt{ }\)[(2004-1)(2004+1)]
= 4008 + 2\(\sqrt{ }\)(2004² - 1) < 2.2004 + 2\(\sqrt{ }\)(2004²) = 4.2004 = B²
\(\Rightarrow\) A < B

Ta có: \(2\sqrt{2003.2005}=2\sqrt{2004^2-1}< 2\sqrt{2004^2}\)

\(\Rightarrow\) 2003 + \(2\sqrt{2003.2005}+2005\) < 2003 + 4008 + 2005

hay \(\left(\sqrt{2003}+\sqrt{2005}\right)^2< 8016\)

\(\Rightarrow\) \(\sqrt{2003}+\sqrt{2005}\) < 2 \(\sqrt{2004}\)

Áp dụng bđt \(\frac{\sqrt{a}+\sqrt{b}}{2}< \sqrt{\frac{a+b}{2}}\) (bạn tự c/m) với a = 2003 , b = 2005

được : \(\frac{\sqrt{2003}+\sqrt{2005}}{2}< \sqrt{\frac{2003+2005}{2}}\)

\(\Rightarrow\sqrt{2003}+\sqrt{2005}< 2\sqrt{2004}\)

Ta có: 4 > 3 ⇒  4  >  3  ⇒ 2 >  3

Suy ra: 2 – 1 >  3  – 1

Vậy 1 > 3  – 1

2 + 3  và  10

Ta có: 2 + 3 2 = 2 + 2 6 + 3 = 5 + 2 6

10 2  = 10 = 5 + 5

So sánh 26 và 5:

Ta có: 2 6 2 = 2 2 . 6 2  = 4.6 = 24

5 2  = 25

Vì 2 6 2 < 5 2  nên 2 6 < 5

Vậy 5 + 2 6  < 5 + 5 ⇒ 2 + 3 2 < 10 2  ⇒  2 + 3 <  10