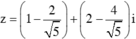Tìm môđun của số phức z thỏa mãn điều kiện z ( 4 - 3 i ) = 2 + z
A. z = 2
B. z = 1 2
C. z = 4
D. z = 3
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
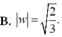
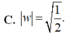
![]()
Trong các số phức thỏa mãn điều kiện z + 3 i = z + 2 - i Tìm số phức có môđun nhỏ nhất ?
A. z = 1 -2i
B. z = - 1 5 + 2 5 i
C. z = 1 5 - 2 5 i
D. z = -1+2i
Trong các số phức thỏa mãn điều kiện | z + 3 i | = | z + 2 - i | . Tìm số phức có môđun nhỏ nhất?
A. z = 1 - 2 i
B. z = - 1 5 + 2 5 i
C. z = 1 5 - 2 5 i
D. z = -1 + 2i
Trong các số phức thỏa mãn điều kiện z - 2 - 4 i = z - 2 i . Tìm môđun nhỏ nhất của số phức z+2i
A. 5
B. 3 5
C. 3 2
D. 3 + 2
Biết số phức z thỏa mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = | z + 2 | 2 - | z - i | 2 đạt giá tri lớn nhất. Tính môđun của số phức z+i
![]()
![]()
![]()
![]()
Trong các số phức z thỏa mãn điều kiện z - 2 - 4 i = z - 2 i .Tìm số phức z có môđun nhỏ nhất
A. z = -2 +2i
B. z = -1 +i
C. z = 3+ 2i
D. z = 2 +2i
Trong các số phức z thỏa mãn điều kiện z - 2 - 4 i = z - 2 i .Tìm số phức z có môđun nhỏ nhất
A. z = -2 +2i
B. z = -1 +i
C. z = 3 +2i
D. z = 2 +2i
Trong các số phức thỏa mãn điều kiện: z - 2 - 4 i = z - 2 i . Tìm số phức z có môđun nhỏ nhất
A. z = 2 +i
B. z = 3 +i
C. z = 2 +2i
D. z = 1 +3i
Trong các số phức z thỏa mãn điều kiện |z – 1 – 2i| = 2, tìm số phức z có môđun nhỏ nhất.
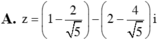
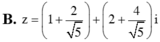
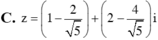
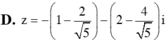
Chọn C.
Gọi z = x + yi và M (x; y) là điểm biểu diễn số phức.
Ta có : |z – 1 – 2i| = 2 hay ( x - 1) 2 + (y - 2)2 = 4
Đường tròn (C): ( x - 1)2 + (y - 2)2 = 4 có tâm I(1; 2). Đường thẳng OI có phương trình y = 2x
Số phức z thỏa mãn điều kiện và có môdun nhỏ nhất khi và chỉ khi điểm biểu diễn số phức đó thuộc đường tròn (C) và gần gốc tọa độ O nhất, điểm đó chỉ là một trong hai giao điểm của đường thẳng OI với (C), khi đó tọa độ của nó thỏa mãn hệ
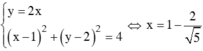 hoặc
hoặc 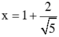
Chọn  nên số phức
nên số phức