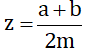Bài 5 (trang 111 SGK Toán 4):
Bài 21 (trang 111 SGK Toán 9 Tập 1)
Cho tam giác $ABC$ có $AB = 3$, $AC = 4$, $BC = 5$. Vẽ đường tròn $(B; BA)$. Chứng minh rằng $AC$ là tiếp tuyến của đường tròn.
Tam giác có:
Mặt khác:
Vậy .
Do đó (định lí Py-ta-go đảo).
vuông góc với bán kính tại nên là tiếp tuyến của đường tròn .
Ta có: AB2 + AC2 = 32 + 42 = 25
BC2 = 52 = 25
Nên AB2 + AC2 = BC2
=> tam giác ABC vuông tại A hay AC ⊥ BA.
Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn.
Bài 5 (trang 118 SGK Toán 4):
AI XEM HỘ MIK BÀI TOÁN SỐ 4 BÀI LUYỆN TẬP TRANG 99 SGK TOÁN LỚP 5
chu vi của hình tròn đó
6x3,14=18,84(cm)
đs:18,84cm
vậy đáp án là A
Bài 4 (trang 137 SGK Toán 4):
Bài 3 (trang 106 SGK Toán 5) Luyện tập chung : Một sợi dây nối hai bánh xe ròng rọc. Đường kính của bánh xe là 0,35m. Hai trục cách nhau 3,1m. Tính độ dài sợi dây.
Độ dài hai phần uốn cong của sợi dây chính là hai nửa chu vi của bánh xe nên đúng bằng chu vi của bánh xe.
Độ dài hai phần thẳng của sợi dây đều bằng khoảng cách giữa hai trục.
Độ dài hai phần uốn cong của sợi dây là:
0,35 x 3,14 = 1,099 (m)
Độ dài hai phần thẳng của sợi dây là:
3,1 x 2 = 6,2 (m).
Độ dài sợi dây là:
1,099 + 3,1 x 2 = 7,299 (m)
Đáp số: 7,299m
Độ dài hai phần uốn cong của sợi dây là:
0,35 x 3,14 = 1,099 (m)
Độ dài hai phần thẳng của sợi dây là:
3,1 x 2 = 6,2 (m)
Độ dài sợi dây là: 1,099 + 3,1 x 2 = 7,299 (m)
Đáp số: 7,299m
Bài 3 (trang 177 SGK Toán 4):

Tính chu vi các hình sau:

Hình đâu bạn ơi ??
# Lieutenant Dm #
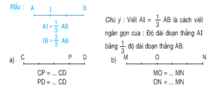
Tìm trong các hình 63, 64 các tam giác bằng nhau ( các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau ). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó. Viết kí hiệu về sự bằng nhau của các tam giác đó .
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ
hinh 63
dinh A = dinh I
dinh C = dinh N
dinh B = dinh M
\(\Rightarrow\)tam giac \(ABC=\)tam giac \(IMN\)
hinh 64
dinh P = dinh H
dinh chua goc \(\widehat{PQR}=\)dinh chua goc \(\widehat{QRH}\)
dinh chua goc \(\widehat{PRQ}=\)dinh cua goc \(\widehat{RQH}\)
\(\Rightarrow\)tam giac \(PQR=\)tam giac \(HRQ\)
Giả sử