Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau: d : x = 12 + 4 t y = 9 + 3 t z = 1 + t α : 3 x + 5 y - z - 2 = 0
Những câu hỏi liên quan
Xét vị trí tương đối của đường thẳng d với mặt phẳng (
α
) trong các trường hợp sau:
d
:
x
2
-
t
y
t
z...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng ( α ) trong các trường hợp sau:
d : x = 2 - t y = t z = 2 + t và ( α ): x + z + 5 = 0
Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của ( α ) ta được: (2 – t) +(2 + t) + 5 = 0 ⇔ 0t = -9
Phương trình vô nghiệm, vậy đường thẳng d song song với ( α )
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng d với mặt phẳng (
α
) trong các trường hợp sau:
d
:
x
t
y
1
+
2
t...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng ( α ) trong các trường hợp sau:
d : x = t y = 1 + 2 t z = 1 - t và ( α ): x + 2y + z - 3 = 0
Thay x, y, z trong phương trình tham số của đường thẳng d vào phương trình tổng quát của mặt phẳng ( α ) ta được: t + 2(1 + 2t) + (1 – t) – 3 = 0
⇔ 4t = 0 ⇔ t = 0
Vậy đường thẳng d cắt mặt phẳng ( α ) tại M 0 (0; 1; 1)
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng d với mặt phẳng (
α
) trong các trường hợp sau:
d
:
x
3
-
t
y
2
-
t...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng ( α ) trong các trường hợp sau:
d : x = 3 - t y = 2 - t z = 1 + 2 t và ( α ): x + y + z - 6 = 0
Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của ( α ) ta được: (3 – t) + (2 – t) + (1 + 2t) – 6 = 0 ⇔ 0t = 0
Phương trình luôn thỏa mãn với mọi t. Vậy d chứa trong ( α ) .
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau:
x
1
+
t
y
2
-
t
z
1...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau: x = 1 + t y = 2 - t z = 1 + 2 t α : x + 3 y + z + 1 = 0
Giao điểm (nếu có) của đường thẳng (d) và mp(α ) là nghiệm hệ phương trình:
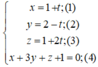
Thay (1); (2); (3) vào (4) ta được:
1 + t + 3(2 – t) + 1 + 2t + 1 = 0
⇔ 0t + 9 = 0
Phương trình vô nghiệm
⇒ (d) không cắt (α).
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau:
d
:
x
1
+
t
y
1
+
2
t
z...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau:
d : x = 1 + t y = 1 + 2 t z = 2 - 3 t α : x + y + z - 4 = 0
Giao điểm (nếu có) của đường thẳng (d) và mp(α) là nghiệm hệ phương trình:
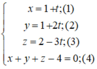
Thay (1); (2); (3) vào (4) ta được:
1 + t + 1 + 2t + 2 – 3t – 4 = 0
⇔ 0t = 0
Phương trình có vô số nghiệm
⇒ (d) ⊂ (α)
hay (d) cắt (α) tại vô số điểm.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
−
1
2
y
+
1
−
1
z
3
và mặt phẳng
(
α
)
:
x
+
5
y
+
z
+
4...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x − 1 2 = y + 1 − 1 = z 3 và mặt phẳng ( α ) : x + 5 y + z + 4 = 0. Xác định vị trí tương đối của d và ( α )
A. d ⊥ ( α ) .
B. d ⊂ ( α ) .
C. d cắt và vuông góc với α
D. d / / ( α ) .
5 tháng 12 2016 lúc 18:09
cho tứ diện ABCD . gọi M , N lần lượt là trung điểm các cạnh AB , AC .
a) xét vị tí tương đối giữa đoạn thẳng MN với mặt phẳng BCD .
b) gọi d là giao tuyến 2 mặt phẳng DMN và DBC . xét vị trí tương đối của d với mặt phẳng ABC .
6 tháng 12 2016 lúc 22:16
cho tứ diện ABCD . gọi M , N lần lượt là trung điểm các cạnh AB , AC .
a) xét vị tí tương đối giữa đoạn thẳng MN với mặt phẳng BCD .
b) gọi d là giao tuyến 2 mặt phẳng DMN và DBC . xét vị trí tương đối của d với mặt phẳng ABC .
3 tháng 12 2016 lúc 19:01
cho tứ diện ABCD . gọi M , N lần lượt là trung điểm các cạnh AB , AC .
a) xét vị tí tương đối giữa đoạn thẳng MN với mặt phẳng BCD .
b) gọi d là giao tuyến 2 mặt phẳng DMN và DBC . xét vị trí tương đối của d với mặt phẳng ABC .