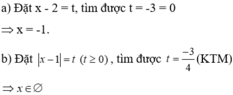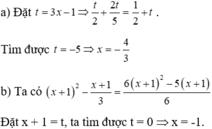Giải các phương trình sau: 13 2 x + 1 - 13 x - 12 = 0

Những câu hỏi liên quan
Giải các phương trình sau bằng cách đưa về phương trình tích x + 1 3 –x +1 = (x -1)(x -2)
Ta có: x + 1 3 –x +1 = (x -1)(x -2)
⇔ x 3 +3 x 2 +3x +1 –x +1 = x 2 -2x –x +2
⇔ x 3 +2 x 2 +5x = 0 ⇔ x( x 2 + 2x + 5) =0
⇔ x =0 hoặc x 2 +2x +5 =0
Giải phương trình x 2 +2x +5 =0
∆ ’ = 1 2 - 1.5 = 1 - 5 = -4 < 0 ⇒ phương trình vô nghiệm
Vậy phương trình đã cho có 1 nghiệm : x=0
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
2
+
x
−
2
2
−
2
x
−
4
3
−
5
6
2
−
x
0
;
b)
x
−
1...
Đọc tiếp
Giải các phương trình sau:
a) 2 + x − 2 2 − 2 x − 4 3 − 5 6 2 − x = 0 ;
b) x − 1 − 2 x − 1 3 = 1 + 2 x − 2 2 .
Giải các phương trình sau:a)
2
x
−
1
3
+
6
3
x
−
1
2
2
x
+
1
3
+
6...
Đọc tiếp
Giải các phương trình sau:
a) 2 x − 1 3 + 6 3 x − 1 2 = 2 x + 1 3 + 6 x + 2 3 ;
b) x − 2 2 + 3 − 2 x 2 − 4 x − 4 x − 5 = x + 3 2 ;
c) x − 3 + 2 x − 3 − 1 3 = 3 − x 4 ;
d) x + 4 3 − 1 7 = 2 − x 7 + x 3 + x + 1 .
Giải các phương trình sau:
1
3
-
x
-
1
x
+
1
x
x
-
3
-
(
x
-
1
)
2
x
2
-
2...
Đọc tiếp
Giải các phương trình sau: 1 3 - x - 1 x + 1 = x x - 3 - ( x - 1 ) 2 x 2 - 2 x - 3
ĐKXĐ: x ≠ - 1;x ≠ 3.
Ta có: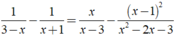
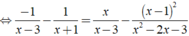
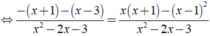
![]()
⇔ -2x + 2 = 3x - 1
⇔ 5x = 3 ⇔ x = 3/5.
Kết hợp điều kiện, vậy phương trình đã cho có nghiệm là x = 3/5.
Đúng 0
Bình luận (0)
Giải các phương trình sau:
1
3
-
x
-
1
x
+
1
x
x
-
3
-
(
x
-
1
)
2
x
2
-
2...
Đọc tiếp
Giải các phương trình sau: 1 3 - x - 1 x + 1 = x x - 3 - ( x - 1 ) 2 x 2 - 2 x - 3
Giải các phương trình sau
a) x^4 – 3x^2 + 6x + 13 = 0
b) x^6 + x^5 + x^4 + x^3 + x^2 + x + 1 = 0
Giải các phương trình sau:a)
3
x
−
1
2
−
2
−
6
x
5
1
2
+
3
x
−
1
;
b)
x
2...
Đọc tiếp
Giải các phương trình sau:
a) 3 x − 1 2 − 2 − 6 x 5 = 1 2 + 3 x − 1 ;
b) x 2 + 2 x + 1 − x + 1 3 = 6 x + 1 2 − 5 x − 5 6 .
Giải các bất phương trình sau và viết tập nghiệm bằng kí hiệu tập hợp:a)
x
+
2
7
−
1
21
3
x
+
1
3
;
b)
1
+
x
−
2
3
5...
Đọc tiếp
Giải các bất phương trình sau và viết tập nghiệm bằng kí hiệu tập hợp:
a) x + 2 7 − 1 21 > 3 x + 1 3 ; b) 1 + x − 2 3 > 5 − x + 3 ( x − 2 ) 3
Giải các phương trình sau
a) x^4 – 3x^2 + 6x + 13 = 0
b) x^6 + x^5 + x^4 + x^3 + x^2 + x + 1 = 0
a, pt <=> (x^4-4x+4)+(x^2+6x+9) = 0
<=> (x^2-2)^2+(x+3)^2=0
<=> x^2-2=0 và x+3=0
=> pt vô nghiệm
b, pt <=> (x-1).(x^6+x^5+x^4+x^3+x^2+x+1) = 0
<=> x^7+x^6+x^5+x^4+x^3+x^2+x-x^6-x^5-x^4-x^3-x^2-x-1 = 0
<=> x^7-1=0
<=> x^7=1 = 1^7
=> x=1
Tk mk nha
Đúng 0
Bình luận (0)
Giải các phương trình sau
x^4 – 3x^2 + 6x + 13 = 0
x4-3x2+6x+13=0
<=> x4-4x2+4+x2+6x+9=0
ta co : x2 - 2 khác x-3
=> phương trình vô nghiệm
Tk mk nha ! m.n.
Đúng 0
Bình luận (0)