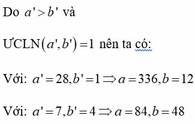Tìm hai số nguyên dương a,b biết: [a,b] = 336 và (a,b) = 12

Những câu hỏi liên quan
Tìm hai số nguyên dương a, b biết: a , b = 336 và a , b = 12 .
Tìm hai số tự nhiên a và b (a > b) biết ƯCLN(a, b) = 12 và BCNN(a, b) = 336.
TK
Ta có : ƯCLN(a,b) . BCNN(a,b) = a.b
⇒a.b=336.12=4032⇒a.b=336.12=4032
Vì ƯCLN (a,b) = 12
⇒{a=12kb=12q(ƯCLN(k,q)=1;k>q)⇒{a=12kb=12q(ƯCLN(k,q)=1;k>q)
Mà : a.b = 4032
⇒12k.12q=4032⇒(12.12)(k.q)=4032⇒12k.12q=4032⇒(12.12)(k.q)=4032
⇒144.k.q=4032⇒k.q=28⇒144.k.q=4032⇒k.q=28
+)
Đúng 1
Bình luận (0)
Ta có : ƯCLN(a,b) . BCNN(a,b) = a.b
⇒a.b=336.12=4032⇒a.b=336.12=4032
Vì ƯCLN (a,b) = 12
⇒{a=12kb=12q(ƯCLN(k,q)=1;k>q)⇒{a=12kb=12q(ƯCLN(k,q)=1;k>q)
Mà : a.b = 4032
⇒12k.12q=4032⇒(12.12)(k.q)=4032⇒12k.12q=4032⇒(12.12)(k.q)=4032
⇒144.k.q=4032⇒k.q=28⇒144.k.q=4032⇒k.q=28
+) ⇒{k=28q=1⇒{a=28.12b=1.12⇒{a=336b=12⇒{k=28q=1⇒{a=28.12b=1.12⇒{a=336b=12
+) ⇒{k=14q=2⇒{a=14.12b=12.2⇒{a=168b=24⇒{k=14q=2⇒{a=14.12b=12.2⇒{a=168b=24
+) ⇒{k=7q=4⇒{a=7.12b=4.12⇒{a=84b=48⇒{k=7q=4⇒{a=7.12b=4.12⇒{a=84b=48
Vậy a = 336 ; b = 12
a = 168 ; b = 24
a = 84 ; b = 48Ta có : ƯCLN(a,b) . BCNN(a,b) = a.b
⇒a.b=336.12=4032⇒a.b=336.12=4032
Vì ƯCLN (a,b) = 12
⇒{a=12kb=12q(ƯCLN(k,q)=1;k>q)⇒{a=12kb=12q(ƯCLN(k,q)=1;k>q)
Mà : a.b = 4032
⇒12k.12q=4032⇒(12.12)(k.q)=4032⇒12k.12q=4032⇒(12.12)(k.q)=4032
⇒144.k.q=4032⇒k.q=28⇒144.k.q=4032⇒k.q=28
+) ⇒{k=28q=1⇒{a=28.12b=1.12⇒{a=336b=12⇒{k=28q=1⇒{a=28.12b=1.12⇒{a=336b=12
+) ⇒{k=14q=2⇒{a=14.12b=12.2⇒{a=168b=24⇒{k=14q=2⇒{a=14.12b=12.2⇒{a=168b=24
+) ⇒{k=7q=4⇒{a=7.12b=4.12⇒{a=84b=48⇒{k=7q=4⇒{a=7.12b=4.12⇒{a=84b=48
Vậy a = 336 ; b = 12
a = 168 ; b = 24
a = 84 ; b = 48
Chúc bạn học tốt nha!
Đúng 1
Bình luận (0)
Ta có :
BCNN(a,b) . ƯCLN(a,b) = a . b = 12 . 336 = 4032
Vì ƯCLN(a,b) = 12
⇒ a = 12x ; b = 12y ; ( x , y) = 1
Thay a = 12x , b = 12y vào a.b = 4032 ta được :
12x . 12y = 4032
12 . 12 . x . y = 4032
144 . x . y = 4032
x . y = 4032 : 144 = 28
⇒ x,y ∈ Ư(28) = {1,2,4,7,14,18} mà x,y = 1 ⇒ (x,y) = (1,28) ; (28;1) ; (7,4) ; (4,7)
Mà a > b ⇒ 12x > 12y ⇒ x > y ⇒ x ∈ {28,7}
+ Nếu x = 28 ⇒ a = 28 . 12 = 336 ; y = 1 ⇒ b = 1 . 12 = 12
+ Nếu x = 7 ⇒ a = 7 . 12 = 84 ; y = 4 ⇒ b = 4 . 12 = 48
Vậy (a,b) = ( 336,12) ; (84,48)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm hai số a và b (a > b) biết BCNN(a,b) = 336 và ƯCLN(a,b)=12
Câu hỏi của Cặp đôi ngọt ngào - Toán lớp 6 - Học toán với OnlineMath
tham khảo nhé!
Đúng 0
Bình luận (0)
Tìm hai số a và b (a > b) biết BCNN(a,b) = 336 và ƯCLN(a,b)=12
Câu hỏi của Cặp đôi ngọt ngào - Toán lớp 6 - Học toán với OnlineMath
tham khảo nhé!
Đúng 0
Bình luận (0)
Tìm hai số tự nhiên a và b biết : BCNN(a,B) = 336 ƯCLN (a,B)=12
Câu hỏi của Cặp đôi ngọt ngào - Toán lớp 6 - Học toán với OnlineMath
Tham khảo!
Đúng 0
Bình luận (0)
Trả lời :
Tham khảo :
Câu hỏi của Cặp đôi ngọt ngào - Toán lớp 6 - Học toán với OnlineMath
Link :
https://olm.vn/hoi-dap/detail/198244172905.html
~HT~
\(ab=\left[a,b\right]\left(a,b\right)=336.12=4032\)
Đặt \(a=12n,b=12m,\left(m,n\right)=1\).
Khi đó \(ab=12m.12n=144mn=4032\Leftrightarrow mn=28\)
Ta có bảng giá trị:
| m | 1 | 4 | 7 | 28 |
| n | 28 | 7 | 4 | 1 |
| a | 12 | 48 | 84 | 336 |
| b | 336 | 84 | 48 | 12 |
1/ a)Cho A 20+21+22+23+24+25 +26 .........+ 299 CMR: A chia hết cho 31 b)tìm số tự nhiên n để 3n+4 chia hết cho n -12/tìm hai số nguyên dương a, b biết [ a,b] 240 và (a,b) 163/tìm hai số nguyên dương a,b biết rằng ab216 và (a ,b)64/tìm hai số nguyên dương a,b biết rằng ab180 , [a,b] 605/tìm hai số nguyên dương a,b biết a/b 2,6 và (a,b) 56/ tìm a,b biết a/b4/5 và [ a,b ] 1407/tìm số nguyên dương a,b biết a+b 128 và (a ,b)168/ a)tìm a,b biết a+b 42 và [a,b] 72 b)tìm a,b biết a-b 7 , [a,b...
Đọc tiếp
1/ a)Cho A= 20+21+22+23+24+25 +26 .........+ 299 CMR: A chia hết cho 31
b)tìm số tự nhiên n để 3n+4 chia hết cho n -1
2/tìm hai số nguyên dương a, b biết [ a,b] = 240 và (a,b) = 16
3/tìm hai số nguyên dương a,b biết rằng ab=216 và (a ,b)=6
4/tìm hai số nguyên dương a,b biết rằng ab=180 , [a,b] =60
5/tìm hai số nguyên dương a,b biết a/b =2,6 và (a,b) =5
6/ tìm a,b biết a/b=4/5 và [ a,b ] = 140
7/tìm số nguyên dương a,b biết a+b = 128 và (a ,b)=16
8/ a)tìm a,b biết a+b = 42 và [a,b] = 72
b)tìm a,b biết a-b =7 , [a,b] =140
9/tìm hai số tự nhiên , biết rằng tổng cúa chúng bằng 100 và có UwCLN là 10
10/ tìm 2 số tự nhiên biết ƯCLN của chúng là 5 và chúng có tích là 300
11/ chứng minh rằng nếu số nguyên tố p> 3 thì (p - 1) . (p + 1) chia hết cho 24
12/ tìm hai số tự nhiên a,b (a < b ) biết ƯCLN (a,b ) = 12 , BCNN(a,b) = 180
BÀI NÀY Ở ĐÂU MÀ NHIỀU THẾ BẠN!?
GIẢI CHẮC ĐÃ LẮM ĐÓ
Đúng 0
Bình luận (0)
câu 1 a) thíu là chứng minh rằng a chia hết cho 31
Đúng 0
Bình luận (0)
Tìm hai số tự nhiên a,b biết a>b và BCNN(a,b) = 336 , UWCLN (a,b)=12
Sách Nâng Cao PT 6
Có : a . b = BCNN(a,b) . ƯCLN(a,b)
=> a . b = 336 . 12 = 4032
Vì ƯCLN(a,b) = 12 nên ta có : a = 12k ; b = 12l ( k, l nguyên tố cùng nhau)
Lại có : a>b nên k > l
=> 12k . 12l = 4032
144 . k . l = 4032
=> k . l = 28 => k;l \(\in\)Ư(28) = { 1;2;4;7;14;28 }
Ta có bảng :
| k | 7 | 28 |
| l | 4 | 1 |
| a =12k | 84 | 336 |
| b =12l | 48 | 12 |
Vậy...
Đúng 0
Bình luận (0)
THAM KHẢO BÀI LÀM CỦA CÁC BẠN:
Câu hỏi của Cặp đôi ngọt ngào - Toán lớp 6 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Ta có: BCNN (a, b) . ƯCLN (a, b) = a . b = 336 . 12 = 4032
Vì ƯCLN (a, b) = 12
\(\Rightarrow\hept{\begin{cases}a=12k\\b=12q\end{cases}(ƯCLN\left(k,q\right)=1;k>q)}\)
Mà a.b = 4032
\(\Rightarrow12k.12q=4032\)
\(\Rightarrow12^2.k.q=4032\)
\(\Rightarrow144.k.q=4032\)
\(\Rightarrow k.q=28\)
Th1: \(\Rightarrow\hept{\begin{cases}k=28\\q=1\end{cases}\Rightarrow}\hept{\begin{cases}a=12.28\\b=12.1\end{cases}\Rightarrow}\hept{\begin{cases}a=336\\b=12\end{cases}}\)
Th2: \(\Rightarrow\hept{\begin{cases}k=7\\q=4\end{cases}\Rightarrow}\hept{\begin{cases}a=7.12\\b=4.12\end{cases}\Rightarrow\hept{\begin{cases}a=84\\b=48\end{cases}}}\)
Th3: \(\Rightarrow\hept{\begin{cases}k=14\\q=2\end{cases}\Rightarrow}\hept{\begin{cases}a=14.12\\q=2.12\end{cases}\Rightarrow\hept{\begin{cases}a=168\\b=24\end{cases}}}\)
Vậy...
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. Tìm số tự nhiên nhỏ nhất khi chia 6,7,9 được số dư lần lượt lá 2,3,5
2.chứng minh n+1 và 3n+4 là hai số nguyên tố cùng nhau
3. tìm a, b biết BCNN(a,b)= 336 và ƯCLN(a,b)= 12
Bài1
a)Tim hai số nguyên dương a va b biết
a.b=216va UWCLN(a,b)=6
b)Tìm hai số nguyên dương a và b biết tích
a.b=180 và BCNN(a,b)=60
c)tìm a và b biết
a\b=2,6va UWCLN(a,b)=5