Chứng minh rằng:
(a + 1)(b + 1)(a + c)(b + c) ≥ 16abc, với a, b, c là những số dương tùy ý.
Chứng minh rằng :
(a+1)(b+1)(a+c)(b+c)≥16abc
với a,b,c là những số dương tùy ý
Áp dụng BĐT Cauchy cho 2 só dương ta có :
\(a+1\ge2\sqrt{a}\)
\(b+1\ge2\sqrt{b}\)
\(a+c\ge2\sqrt{ac}\)
\(b+c\ge2\sqrt{bc}\)
Nhân vế theo vế các BĐT cùng chiều trên ta được :
\(\left(a+1\right)\left(b+1\right)\left(a+c\right)\left(b+c\right)\ge16\sqrt{a^2b^2c^2}=16abc\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}a=1\\b=1\\c=a\end{cases}}\)
b =c
\(\Leftrightarrow a=b=c=1\)
Vậy \(\left(a+1\right)\left(b+1\right)\left(a+c\right)\left(b+c\right)\ge16abc\) với a,b,c dương
Dấu " = " xảy ra khi \(a=b=c=1\)
Chúc bạn học tốt !!!
Chứng minh rằng :
\(a+b+c\le\dfrac{1}{2}\left(a^2b+b^2c+c^2a+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\)
với a, b, c là những số dương tùy ý
Áp dụng bất đẳng thức Cauchy - Schwarz
\(\Rightarrow\left\{{}\begin{matrix}a^2b+\dfrac{1}{b}\ge2\sqrt{\dfrac{a^2b}{b}}=2a\\b^2c+\dfrac{1}{c}\ge2\sqrt{\dfrac{b^2c}{c}}=2b\\c^2a+\dfrac{1}{a}\ge2\sqrt{\dfrac{c^2a}{a}}=2c\end{matrix}\right.\)
\(\Rightarrow a^2b+b^2c+c^2a+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge2\left(a+b+c\right)\)
\(\Rightarrow\dfrac{1}{2}\left(a^2b+b^2c+c^2a+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge a+b+c\) ( đpcm )
Dấu " = " xảy ra khi \(a=b=c=1\)
Chứng minh rằng :
\(a+b+c\le\frac{1}{2}\left(a^2b+b^2c+c^2a+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
với a, b, c là những số dương tùy ý
Áp dụng bất đẳng thức Cauchy - Schwarz
\(\Rightarrow\hept{\begin{cases}a^2b+\frac{1}{b}\ge2\sqrt{\frac{a^2b}{b}}=2a\\b^2c+\frac{1}{c}\ge2\sqrt{\frac{b^2c}{c}}=2b\\c^2a+\frac{1}{a}\ge2\sqrt{\frac{c^2a}{a}}=2c\end{cases}}\)
\(\Rightarrow a^2b+b^2c+c^2a+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge2\left(a+b+c\right)\)
\(\frac{\Rightarrow1}{2}\left(a^2b+b^2c+c^2a+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge a+b+c\left(đpcm\right)\)
Dấu " = " xảy ra khi \(a=b=c=1\)
Chúc bạn học tốt !!!
\(a^2b+\frac{1}{b}-2a\ge2\sqrt{\frac{a^2b}{b}}-2a=0\)\(\Leftrightarrow\)\(\frac{1}{2}\left(a^2b+\frac{1}{b}\right)\ge a\)
phần còn lại mình dành cho bạn :)
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
![]()
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
![]()
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
![]()
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
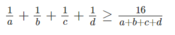
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
![]()
Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:
![]()