Tìm m để hàm số sau có giới hạn khi x → 1.
f x = x 2 + x - 2 1 - x + m x + 1 k h i x < 1 3 m x + 2 m - 1 k h i x ≥ 1
A. 2 3
B. 2 5
C. 3 2
D. 1 2
Những câu hỏi liên quan
Tìm a để hàm số sau có giới hạn khi
x
→
2
f
(
x
)
x
2
+
a
x
+
2
khi
x
2...
Đọc tiếp
Tìm a để hàm số sau có giới hạn khi x → 2
f ( x ) = x 2 + a x + 2 khi x > 2 2 x 2 − x + 1 khi x ≤ 2
A. + ∞
B. − ∞
C. 1 2
D.1
Chọn C.
Ta có:
lim x → 2 + f ( x ) = lim x → 2 + ( x 2 + a x + 2 ) = 2 a + 6 .
lim x → 2 − f ( x ) = lim x → 2 − ( 2 x 2 − x + 1 ) = 7 .
Hàm số có giới hạn khi x → 2 ⇔ lim x → 2 + f ( x ) = lim x → 2 − f ( x ) ⇔ 2 a + 6 = 7 ⇔ a = 1 2 .
Vậy a = 1 2 là giá trị cần tìm.
Đúng 0
Bình luận (0)
Tìm a để hàm số
f
(
x
)
x
2
+
a
x
+
2
,
x
1
2
x
2
-...
Đọc tiếp
Tìm a để hàm số f ( x ) = x 2 + a x + 2 , x > 1 2 x 2 - x + 3 a , x ≤ 1 có giới hạn khi x → 1.
A. 2
B. 3
C. -1
D. 1
- Ta có:
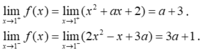
- Hàm số có giới hạn khi:
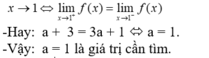
Chọn D.
Đúng 0
Bình luận (0)
Tìm m để các hàm số
f
(
x
)
x
2
+
m
x
+
2
m
+
1
x
+...
Đọc tiếp
Tìm m để các hàm số f ( x ) = x 2 + m x + 2 m + 1 x + 1 k h i x ≥ 0 2 x + 3 m - 1 1 - x + 2 k h i x < 0 có giới hạn khi x → 1
Ta có:
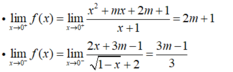
- Hàm số có giới hạn khi x → 1 khi và chỉ khi:
Đúng 0
Bình luận (0)
Tìm a để hàm số
f
(
x
)
5
a
x
2
+
3
x
+
2
a
+
1
k...
Đọc tiếp
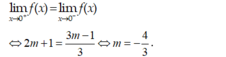
Tìm a để hàm số f ( x ) = 5 a x 2 + 3 x + 2 a + 1 k h i x ≥ 0 1 + x + x 2 + x + 2 k h i x < 0 có giới hạn tại x → 0
A. +∞
B. -∞
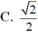
D. 1
Tìm a để hàm số
f
(
x
)
x
2
+
a
x
+
1
k
h
i
...
Đọc tiếp
Tìm a để hàm số f ( x ) = x 2 + a x + 1 k h i x > 1 2 x 2 - x + 3 a k h i x ≤ 1 có giới hạn khi x → 1.
A. +∞
B. -∞
C. -1/6
D. 1
Chọn D.
Ta có: 
Hàm số có giới hạn khi 
⇔ a + 3 = 3a + 1 ⇔ a = 1.
Vậy a = 1 là giá trị cần tìm.
Đúng 0
Bình luận (0)
Tìm a để hàm số sau có giới hạn khi
lim
x
→
2
f
(
x
)
x
2
+
a
x
+
1
k
h...
Đọc tiếp
Tìm a để hàm số sau có giới hạn khi lim x → 2 f ( x ) = x 2 + a x + 1 k h i x > 2 2 x 2 - x + 1 k h i x ≤ 2
A. +∞
B. -∞
C. 1/2
D. 1
Chọn C.
Ta có:
.
Hàm số có giới hạn khi 
Vậy a = 1/2 là giá trị cần tìm.
Đúng 0
Bình luận (0)
Tìm m để hàm số sau có giới hạn khi x → 1:
f
x
x
2
+
x
-
2
1
-
x
+
m
x...
Đọc tiếp
Tìm m để hàm số sau có giới hạn khi x → 1: f x = x 2 + x - 2 1 - x + m x + 1 k h i x < 1 3 m x + 2 m - 1 k h i x ≥ 1
A. m = 2 3
B. m = 2 5
C. m = 3 2
D. m = 1 2
- Ta có:
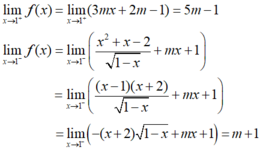
- Hàm số có giới hạn khi x → 1 khi và chỉ khi:
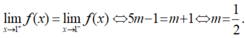
Chọn D.
Đúng 0
Bình luận (0)
Tìm m để các hàm số
f
(
x
)
x
2
+
m
x
+
2
m
+
1
x
+...
Đọc tiếp
Tìm m để các hàm số f ( x ) = x 2 + m x + 2 m + 1 x + 1 k h i x ≥ 0 2 x + 3 m - 1 1 - x + 2 k h i x < 0 có giới hạn khi x → 0.
A. 1 3
B. - 1 3
C. - 2 3
D. - 4 3
- Ta có:
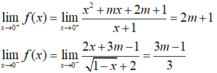
- Hàm số có giới hạn khi x → 0 khi và chỉ khi:
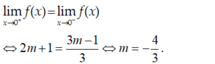
Chọn D.
Đúng 0
Bình luận (0)
Với giá trị nào của m thì hàm số sau có giới hạn x dần đến 1. Tìm giới hạn đó
\(f\left(x\right)=\left\{{}\begin{matrix}x^2-x+3\Leftrightarrow x\le1\\\dfrac{x+m}{x}\Leftrightarrow x>1\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow1^-}x^2-x+3=1^2-1+3=3\)
\(\lim\limits_{x\rightarrow1^+}\dfrac{x+m}{x}=\dfrac{1+m}{1}=m+1\)
Để tồn tại \(\lim\limits_{x\rightarrow1}f\left(x\right)\) thì \(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\)
\(\Leftrightarrow m+1=3\Leftrightarrow m=2\)
Vậy ...
Đúng 2
Bình luận (0)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Leftrightarrow\lim\limits_{x\rightarrow1^+}\dfrac{x+m}{x}=\lim\limits_{x\rightarrow1^-}\left(x^2-x+3\right)\\ \Leftrightarrow m+1=3\Leftrightarrow m=2\)
Đúng 1
Bình luận (0)