Nối hai số có tổng bằng 90:
Cho hình thang có tổng hai góc ở một đáy bằng 900 . Chứng minh rằng : Đoạn thẳng nối trung điểm hai đáy có độ dài bằng nửa hiệu độ dài hai đáy.
Hai số có tổng bằng 90, số hạng thứ hai bằng 90 . Vậy số hạng thứ nhất bằng:
A. 3
B. 1
C. 2
D. 0
Lời giải
Vì 0 + 90 = 90
Nên số hạng thứ nhất bằng 0
Cho hình thang có tổng hai góc ở một đáy bằng \(90\) độ. CMR: Đoạn thẳng nối trung điểm hai đáy có độ dài bằng nửa hiệu độ dài hai đáy.
Kết luận nào sau đây đúng ?
A. Hai góc kề nhau có tổng số đo bằng 90 độ
B. Hai góc phụ nhau có tổng số đo bằng 180 độ
C. Hai góc bù nhau có tổng số đo bằng 90 độ
D. Hai góc bù nhau có tổng số đo bằng 180 độ
Kết luận nào sau đây đúng ?
A. Hai góc kề nhau có tổng số đo bằng 90 độ
B. Hai góc phụ nhau có tổng số đo bằng 180 độ
C. Hai góc bù nhau có tổng số đo bằng 90 độ
D. Hai góc bù nhau có tổng số đo bằng 180 độ
Kết luận nào sau đây đúng ?
A. Hai góc kề nhau có tổng số đo bằng 90 độ
B. Hai góc phụ nhau có tổng số đo bằng 180 độ
C. Hai góc bù nhau có tổng số đo bằng 90 độ
D. Hai góc bù nhau có tổng số đo bằng 180 độ
Chứng minh rằng nếu một hình thang có tổng 2 góc kề một đáy bằng 90o thì đoạn thẳng nối trung điểm 2 đáy bằng nửa hiệu hai đáy.
Lấy P và Q lần lượt là trung điểm của OB và OC.
Xét \(\Delta\)BOC có: D là trung điểm của BC; P là trung điểm của OB => DP là đường trung bình \(\Delta\)BOC
=> DP // OC và DP = 1/2.OC. Mà Q là trung điểm OC => DP // OQ và DP = OQ
Xét tứ giác DPOQ có: DP // OQ; DP = OQ => Tứ giác DPOQ là hình bình hành
=> ^DPO = ^DQO (1)
Xét \(\Delta\)BHO: ^OHB = 900; P là trung điểm OB => HP = OP = BP
Lại có: Tứ giác DPOQ là hbh (cmt) => OP = DQ => HP = DQ
Tương tự ta cũng có: DP = KQ
Mặt khác: HP = BP (cmt) => \(\Delta\)BHP cân tại P
Xét \(\Delta\)BHP cân đỉnh P có góc ngoài là ^HPO => ^HPO = 2.^HBP = 2.^ABO (2)
Tương tự: ^KQO = 2.^ACO (3)
Từ (2) và (3) kết hợp với ^ABO = ^ACO (gt) => ^HPO = ^KQO (4)
Từ (1) và (4) suy ra ^DPO + ^HPO = ^DQO + ^KQO => ^HPD = ^DQK
Xét \(\Delta\)PHD và \(\Delta\)QDK có: DP = KQ; HP = DQ; ^HPD = ^DQK => \(\Delta\)HPD = \(\Delta\)QDK (c.g.c)
=> HD = DK (2 cạnh tương ứng) => \(\Delta\)HDK cân ở D
Xét \(\Delta\)HDK cân đỉnh D có M là trung điểm cạnh HK => DM vuông góc HK (đpcm).
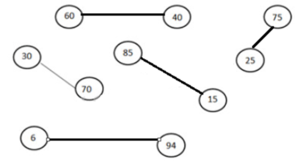
Nối hai số có tổng bằng 100 (theo mẫu):
Phương pháp giải:
Chọn và nối các số có tổng là 100.
Lời giải chi tiết:
tổng 2 góc đáy bằng 90 độ. CMR đoạn thẳng nối chung điểm của hai đáy bằng nửa hiệu đáy của hình thang
Tổng của 2 số bằng 90; biết nếu giảm số thứ nhất đi 10%, số thứ hai đi 20% ta được hai số mới có tổng bằng 76. Tìm hai số đó
số thứ nhất 40 số thứ hai 50 nhé chắc chắn luôn
tổng của hai số bằng 90,biết nếu giảm số thứ nhất đi10/100,số thứ hai đi 20/100 ta được hai số mới có tổng bằng 76 .tìm hai số đó
gọi hai số là a là số thứ nhất & b là số thứ 2. ta có: a + b = 90 --> a = 90 - b
Nếu số thứ nhất giảm đi 10% = 0,1 --> còn lại 0,9a
số thứ 2 giảm đi 20% = 0,2 --> còn lại 0,8b, khi đó ta có tổng mới: 0,9a + 0,8b = 76
<=> 9a + 8b = 760 mà a = 90 -b --> 9(90-b) + 8b = 760
<=> 810 - 9b + 8b = 760
--> b = 810 - 760 = 50
a = 90 - 50 = 40