Cho đa giác đều có 14 cạnh. Tính : Tổng số đo góc của đa giác đó

Những câu hỏi liên quan
Cho đa giác đều có 14 cạnh. Tính : Tổng số đo góc của đa giác đó
Tổng số đo các góc của đa giác n cạnh là ( n - 2 ) . 180 0 .
Tổng số đo của đa giác 14 cạnh là ( 14 - 2 ) . 180 0 = 2160 0 .
Đúng 0
Bình luận (0)
Cho đa giác 8 cạnh
a) Tính số đường chéo của đa giác đó
b) Tính tổng số đo các góc của đa giác đó
c) Tính số đo mỗi góc của đa giác đó nếu đa giác đó đều.
a) Số đường chéo của đa giác đó :
\(\frac{\left(8-3\right).8}{2}=20\)( đường chéo )
b) Tổng số đo các góc của đa giác là :
\(108.\left(8-2\right)=108.6=1080\)độ
c) Số đo mỗi góc của đa giác đều 8 cạnh :
\(1080:8=135\)độ
Đúng 0
Bình luận (0)
Cho đa giác đều có 14 cạnh. Tính : Số đo một góc của đa giác
Số đo của một góc của đa giác đều n cạnh là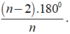
Số đo một góc của đa giác 14 cạnh là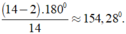
Đúng 0
Bình luận (0)
Cho đa giác đều có 14 cạnh. Tính: Số đo một góc của đa giác
Số đo của một góc của đa giác đều n cạnh là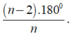
Số đo một góc của đa giác 14 cạnh là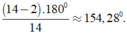
Đúng 0
Bình luận (0)
Một đa giác đều có tổng số đo tất cả các góc ngoài và một góc trong của đa giác đó bằng 468 0 . Hỏi đa giác đều đó có mấy cạnh?
Tổng số đo các góc ngoài của đa giác bằng 360 0
Số đo một góc trong của đa giác đều là 468 0 – 360 0 = 108 0
Gọi n là số cạnh của đa giác đều. Ta có số đo mỗi góc của đa giác đều bằng 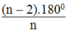
Suy ra: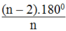 =
108
0
⇒ 180.n – 360 = 108.n⇒ 72n = 360⇒ n = 5
=
108
0
⇒ 180.n – 360 = 108.n⇒ 72n = 360⇒ n = 5
Vậy đa giác đều cần tìm có 5 cạnh.
Đúng 0
Bình luận (0)
Một đa giác đều có tổng số đo tất cả các góc ngoài và một góc trong của đa giác là 468 0 . Hỏi đa giác đều đó có mấy cạnh?
A.5
B. 4
C. 6
D. 3
Gọi n là số cạnh của đa giác đều cần tìm (n ≥ 3)
Mỗi góc trong của đa giác đều có số đo
( n − 2 ) 180 ° n
Tổng số đo các góc ngoài của một đa giác là 3600
Theo bài ra ta có phương trình:
3600 + ( n − 2 ) 180 ° n = 4680
ó = 4680 - 3600
ó = 1080
ó 1800.n – 3600 = 1080 .n
ó 1800.n – 1080 .n = 3600
ó 720.n = 3600
ó n = 3600: 720
ó n = 5
Vậy đa giác đề cần tìm có 5 cạnh.
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Một đa giác đều có tổng số đo tất cả các góc ngoài và một góc trong của đa giác là 480 0 . Hỏi đa giác đều đó có mấy cạnh?
A. 5
B. 4
C. 6
D. 3
Gọi n là số cạnh của đa giác đều cần tìm (n ≥ 3)
Mỗi góc của đa giác đều có số đo
( n − 2 ) 180 ° n
Tổng số đo các góc ngoài của một đa giác là 3600
Theo bài ra ta có phương trình:
3600 + ( n − 2 ) 180 ° n = 4800
ó = 4800 - 3600
ó = 1200
ó 1800.n – 3600 = 1200 .n
ó 1800.n – 1200 .n = 3600
ó 600.n = 3600
ó n = 3600: 600
ó n = 6
Vậy đa giác đề cần tìm có 6 cạnh.
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
Cho một đa giác đều có 20 cạnh. Tính số đo một góc và số đường chéo của đa giác đều đó?
Hướng dẫn:
+ Số đo của một góc của đa giác đều n cạnh là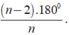
Khi đó số đo của một góc của đa giác đều 20 cạnh là:
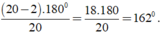
+ Số đường chéo của đa giác n cạnh là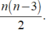
Khi đó số đường chéo của đa giác đều 20 cạnh là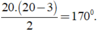
Đúng 0
Bình luận (0)
Phần tự luận (7 điểm)
a) Một đa giác đều có tổng số đo góc ngoài và một góc trong của đa giác bằng 468 o . Hỏi đa giác đó có mấy cạnh?
b) Cho ΔABC vuông tại A, biết AB = 6cm, BC = 10cm. Tính diện tích tam giác ABC.
a) Gọi số cạnh của đa giác đều là n
Một góc trong của đa giác đều n-cạnh có số đo là

Tổng số đo các góc ngoài của đa giác đều n-cạnh là 360o
Ta có:
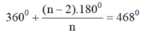
=> n(360o + 180o - 468o) = 360o
<=> n.72o = 360o
<=> n = 5
Vậy đa giác đều có 5 cạnh.
b) Ta có: AB2 + AC2 = BC2 (Py-ta-go)
<=> 62 + AC2 = 102
=> AC2 = 64 => AC = 8 (cm)
Diện tích tam giác ABC là: (6.8)/2 = 24 (cm2)
Đúng 0
Bình luận (0)




