Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = 4 x + 4 2 x + 1

Những câu hỏi liên quan
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y = - x + 2 x + 2
y = - x + 2 x + 2
+) Tập xác định: D = R\{-2}
+) Ta có: 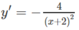
Bảng biến thiên:
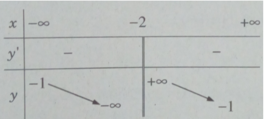
Hàm số nghịch biến trên các khoảng (− ∞ ; −2), (−2; + ∞ )
+) Tiệm cận đứng x = -2 vì
![]()
Tiệm cận ngang y = -1 vì
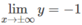
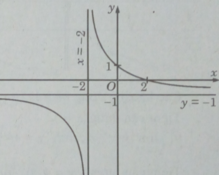
Giao với các trục tọa độ: (0; 1); (2; 0)
Đồ thị
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = x + 3 x + 1
Khảo sát hàm số 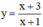
- TXĐ: D = R \ {-1}
- Sự biến thiên:
+ Chiều biến thiên:
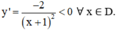
⇒ Hàm số nghịch biến trên các khoảng (-∞; -1) và (-1; +∞).
+ Cực trị: Hàm số không có cực trị.
+ Tiệm cận:
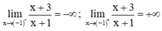
⇒ x = -1 là tiệm cận đứng của đồ thị hàm số.
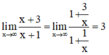
⇒ y = 3 là tiệm cận đứng của đồ thị hàm số.
+ Bảng biến thiên:
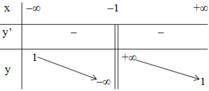
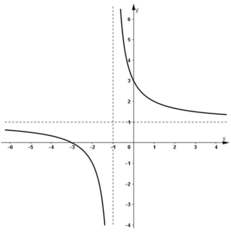
- Đồ thị:
+ Giao với Ox: (-3; 0)
+ Giao với Oy: (0; 3)
+ Đồ thị hàm số nhận (-1; 1) là tâm đối xứng.
Đúng 0
Bình luận (0)
Cho hàm số y = 2 2 - x
Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số đã cho.
Hàm số 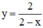
- Tập xác định: D = R\{2}
- Sự biến thiên:
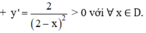
⇒ Hàm số đồng biến trên (-∞; 2) và (2; +∞).
+ Cực trị : Hàm số không có cực trị
+ Tiệm cận: 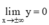
⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
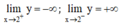
⇒ x = 2 là tiệm cận đứng của đồ thị hàm số.
+ Bảng biến thiên:
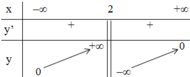
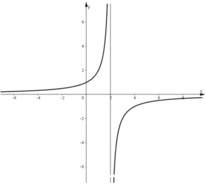
- Đồ thị:
Đúng 0
Bình luận (0)
Cho hàm số y = - 1 3 x 3 + a - 1 x 2 + a + 3 x - 4
Khảo sát sự biến thiên và vẽ đồ thị (C) của đồ thị hàm số a=0
Với a = 0 ta có hàm số 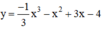
- Tập xác định : D = R.
- Sự biến thiên :
y’ = -x2 – 2x + 3 ;
y’ = 0 ⇔ x = -3 hoặc x = 1.
QUẢNG CÁOBảng biến thiên :
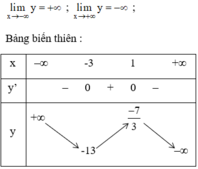
Kết luận :
Hàm số đồng biến trên (-3 ; 1)
Hàm số nghịch biến trên (-∞; -3) và (1; +∞).
Hàm số đạt cực đại tại x = 1 ; 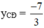
Hàm số đạt cực tiểu tại x = -3 ; yCT = -13.
- Đồ thị hàm số :
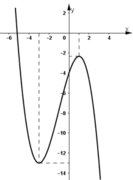
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số: y = x - 3
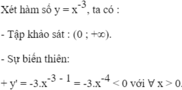
Do đó, hàm số đã cho nghịch biến trên tập xác định.
+ Giới hạn:
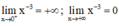
⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số
y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên:
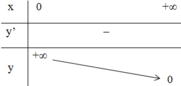
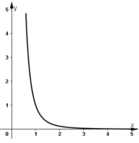
- Đồ thị:
Đúng 0
Bình luận (0)
Cho hàm số y = x - 2 x + m - 1
Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số khi m = 2
Với m = 2 ta có hàm số 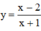
- Tập xác định : D = R\{-1}.
- Sự biến thiên :
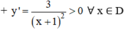
⇒ Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞).
+ Cực trị : hàm số không có cực trị
+ Tiệm cận :

⇒ y = 1 là tiệm cận ngang của đồ thị hàm số
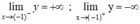
⇒ x = -1 là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên :
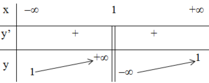
- Đồ thị :
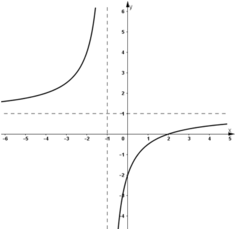
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: y = x - 3
Tập xác định: R\{0}
Hàm số đã cho là hàm số lẻ.
![]()
Ta có: y′ < 0, ∀ x ∈ R \ {0} nên hàm số luôn nghịch biến trên các khoảng xác định.
![]()
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.
Bảng biến thiên:
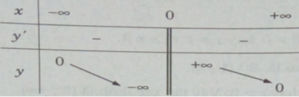
Đồ thị của hàm số có tâm đối xứng là gốc tọa độ.
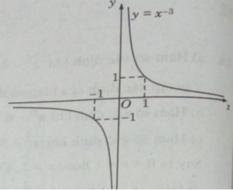
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: y = x - 1 2
Tập xác định: D = (0; + ∞ )
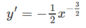
Vì y' < 0 ∀ x ∈ D nên hàm số nghịch biến.
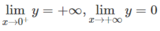
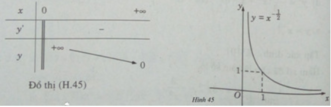
Đồ thị có tiệm cận đứng là trục tung, tiệm cận ngang là trục hoành.
Bảng biến thiên:
Đúng 0
Bình luận (0)
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y = 1 2 x 4 - 3 x 2 + 3 2
Khảo sát hàm số y = 1 2 x 4 - 3 x 2 + 3 2
- TXĐ: D = R
- Sự biến thiên:
+ Chiều biến thiên:
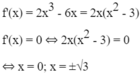
+ Giới hạn tại vô cực:
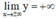
+ Bảng biến thiên:
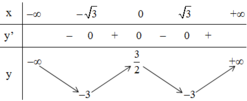

Hàm số đạt cực đại tại x = 0, yCĐ = 3 2
Hàm số đạt cực tiểu tại x = 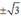 ; yCT = -3.
; yCT = -3.
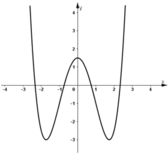
- Đồ thị:
+ Đồ thị hàm số nhận trục tung là trục đối xứng.
+ Đồ thị cắt trục tung tại (0; 1,5).
Đúng 0
Bình luận (0)


