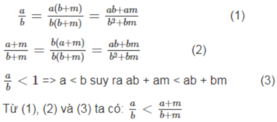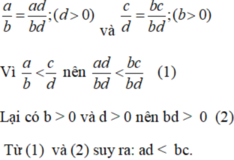Cho a > 0, b > 0, nếu a < b, hãy chứng tỏ: a 2 < ab và ab < b 2

Những câu hỏi liên quan
a) Cho hai phân số:
a
b
và
a
c
có
a b + c (a, b, c
∈
Z, b
≠
0, c
≠
0
)
Chứng tỏ rằng:
a
b
.
a
c
a
b
+
a
c
b) Hãy kiểm tra lại với
a...
Đọc tiếp
a) Cho hai phân số: a b và a c có a = b + c (a, b, c ∈ Z, b ≠ 0, c ≠ 0 )
Chứng tỏ rằng: a b . a c = a b + a c
b) Hãy kiểm tra lại với a = 12 ; b = − 5 .
a)
a b . a c = a 2 b c a b + a c = a c + a b b c = a ( b + c ) b c = a 2 b c ⇒ a b . a c = a b + a c
b)
a = 12 ; b = − 5 ⇒ c = 17 12 − 5 . 12 17 = − 144 85 12 − 5 + 12 17 = − 204 85 + 60 85 = − 144 85 ⇒ 12 − 5 . 12 17 = 12 − 5 + 12 17
Đúng 0
Bình luận (0)
Cho \(a>0,b>0\), nếu \(a< b\) hãy chứng tỏ :
a) \(a^2< ab\) và \(ab< b^2\)
b) \(a^2< b^2\) và \(a^3< b^3\)
a. Do \(a>0,\) \(b>0\) \(\Rightarrow a,b\) là số dương
Ta có:
* \(a< b\Leftrightarrow a^2< ab\) (nhân cả hai vế với a)
* \(a< b\Leftrightarrow ab< b^2\) (nhân cả hai vế với b)
b. Từ câu a theo tính chất bắc cầu suy ra:\(a^2< b^2\)
Ta có: \(a^2< b^2\Leftrightarrow a^3< ab^2\) (nhân cả hai vế với a)
mà ab2<b3 (a<b)
\(\Rightarrow a^3< b^3\)
Đúng 0
Bình luận (0)
Cho a > 0, b > 0, nếu a < b, hãy chứng tỏ: a 2 < b 2 và a 3 < b 3
Từ (1) và (2) suy ra: a 2 < b 2
Ta có: a < b ⇒ a 3 < a 2 b (3)
a < b ⇒ a b 2 < b 3 (4)
a < b ⇒ a.a.b < a.b.b ⇒ a 2 b < a b 2 (5)
Từ (3), (4) và (5) ⇒ a 3 < b 3
Đúng 0
Bình luận (0)
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b > 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b > a + m b + m
Ta có: 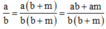
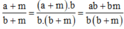
Ta có: a/b > 1 nên a > b suy ra am > bm, suy ra ab + am > ab + bm.
Do đó 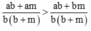
Hay 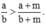
Đúng 0
Bình luận (0)
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b < 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b < a + m b + m
a) Cho phân số
a
b
(
a
,
b
∈
ℕ
,
b
≠
0
)
.Giả sử
a
b
1 và
m
∈
ℕ
,
m
≠
0
. Chứng tỏ rằng
a
b
a
+
m
b
+
m
.b) Áp dụng so sánh:
437
564...
Đọc tiếp
a) Cho phân số a b ( a , b ∈ ℕ , b ≠ 0 ) .Giả sử a b <1 và m ∈ ℕ , m ≠ 0 . Chứng tỏ rằng a b < a + m b + m .
b) Áp dụng so sánh: 437 564 v à 446 573 .
a) Thực hiện quy đồng a b = a ( b + m ) b ( b + m ) = a b + a m b 2 + b m ;
a + m b + m = b ( a + m ) b ( b + m ) = a b + b m b 2 + b m . Vì a b < 1=> a < b => ab +am < ab + bm
Từ đó thu được a b < a + m b + m
b) 437 564 < 437 + 9 564 + 9 = 446 573 .
Đúng 0
Bình luận (0)
Cho a + b + c = 0 và a.b.c khác 0. Chứng tỏ rằng a2/ bc + b2/ ca + c2/ ab = 3
cho a, b là hai số tự nhiên, chứng minh rằng
a) nếu ab=0 thì a=0 hoặc b=0
b) nếu ab=1 thì a=1 và b=1
Cho hai số hữu tỉ a/b và c/d(b > 0, d> 0). Chứng tỏ rằng: ab < bc