Cho hàm số y = - 4 x 3 + 4 x . Để y ' ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây ?
A. - 3 ; 3
B. - 1 3 ; 1 3
C. ( - ∞ ; - 3 ] ∪ [ 3 ; + ∞ )
D. ( - ∞ ; - 1 3 ] ∪ [ 1 3 ; + ∞ )
Cho hàm số y = (2x2 + 1)3. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây?
A. ∅.
B. (-∞; 0].
C. [0; +∞).
D. R
Chọn C.
Ta có: y = (2x2 + 1)3 ⇒ y’ = 12x(2x2 + 1)2 ⇒ y’ ≥ 0 ⇔ x ≥ 0.
Cho hàm số y = -4x3 + 4x. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây
![]()
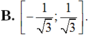
![]()
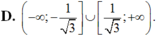
Chọn B.
Ta có y = -4x3 + 4x ⇒ y’ = -12x2 + 4.
Nên 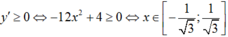
Cho hàm số ![]() . Để y’ > 0 thì x nhận các giá trị thuộc tập nào sau đây?
. Để y’ > 0 thì x nhận các giá trị thuộc tập nào sau đây?
A. (-∞; +∞).
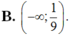
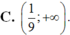
D. ∅.
Cho hàm số ![]() . Để y’ ≤ 0 thì x nhận các giá trị thuộc tập nào sau đây?
. Để y’ ≤ 0 thì x nhận các giá trị thuộc tập nào sau đây?
A. ∅.
B. (-∞; 0).
C. (0; +∞).
D. (-∞; 0].
Cho hàm số y = ( m – 5 ) x – 4 . Tìm m để hàm số nhận giá trị là 5 khi x = 3
A. m = 6
B. m = 7
C. m = 8
D. m = − 3
Thay x = 3 ; y = 5 vào hàm số y = ( m – 5 ) x – 4 ta được:
( m – 5 ) . 3 – 4 = 5 ⇔ ( m – 5 ) . 3 = 9 ⇔ m – 5 = 3 ⇔ m = 8
Vậy m = 8
Đáp án cần chọn là: C
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Cho hàm số y = x 3 - 2 x 2 - 1 (1) và các mệnh đề
(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3
(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3
(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3
(4) Cực trị của hàm số (1) là x = 0 và x = 4/3
Trong các mệnh đề trên, số mệnh đề sai là:
A. 0
B. 1
C. 2
D. 3
Chọn D
Ta có: y ' = 3 x 2 - 4 x , y ' ' = 6 x - 4 ;
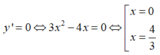
y''(0) = -4 < 0; y''(4/3) = 4 > 0. Do đó hàm số có hai cực trị là x = 0 và x = 4/3
Các mệnh đề (1); (2) và (3) sai;mệnh đề (4) đúng.
Hàm số y được cho bảng sau:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 0 | 2 | 4 | 6 | 8 |
Viết tất cả các cặp giá trị tương ứng (x; y) của hàm số trên
Tất cả các cặp giá trị tương ứng (x; y) là
(0; 0) ; (1; 2) ; (2; 4) ; (3; 6) ; (4; 8)
Cho hàm số y = x + 1 1 - x và các mệnh đề sau
(1) Hàm số trên nhận điểm I(1;-1) làm tâm đối xứng,
(2) Hàm số trên nhận đường thẳng y = -x làm trục đối xứng.
(3) Hàm số trên nhận y = -1 là tiệm cận đứng.
(4) Hàm số trên luôn đồng biến trên R.
Trong số các mệnh đề trên, số mệnh đề sai là
A. 1
B. 2
C. 3
D. 4
Chọn B
+ Hàm số có tiệm cận đứng x=1 và tiệm cận ngang y= -1. Giao điểm của hai đường tiệm cận là I(1; -1) là tâm đối xứng của đồ thị. Mệnh đề 1 đúng, mệnh đề 3 sai.
+ Vì đường thẳng y=-x là một phân giác của góc tạo bởi 2 đường tiệm cận nên đường thẳng y=-x là một trục đối xứng của đồ thị hàm số. Mệnh đề 2 đúng.
+ Hàm số có tập xác định là R\{1}, nên hàm số không thể luôn đồng biến trên R.Mệnh đề 4 sai.