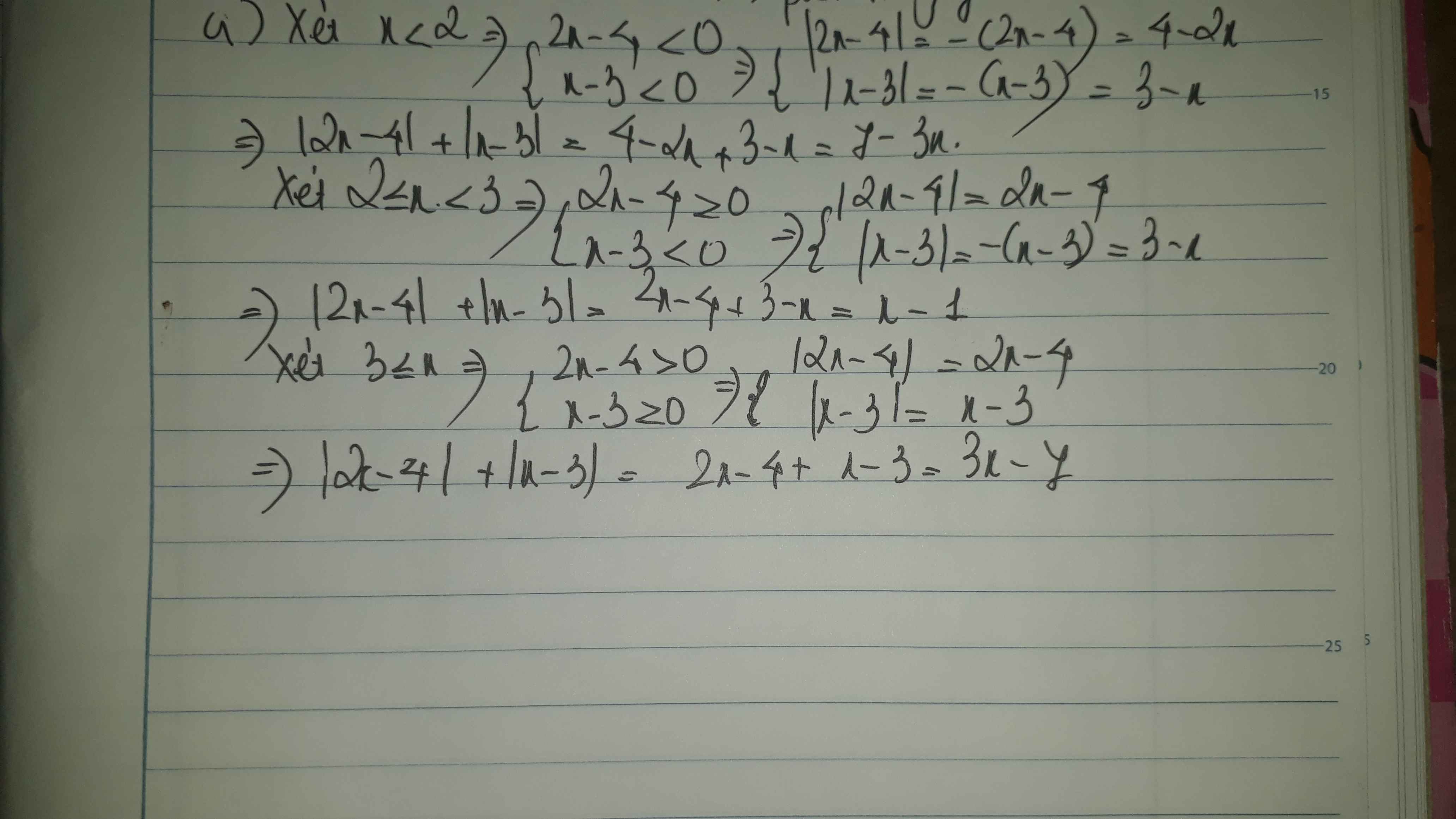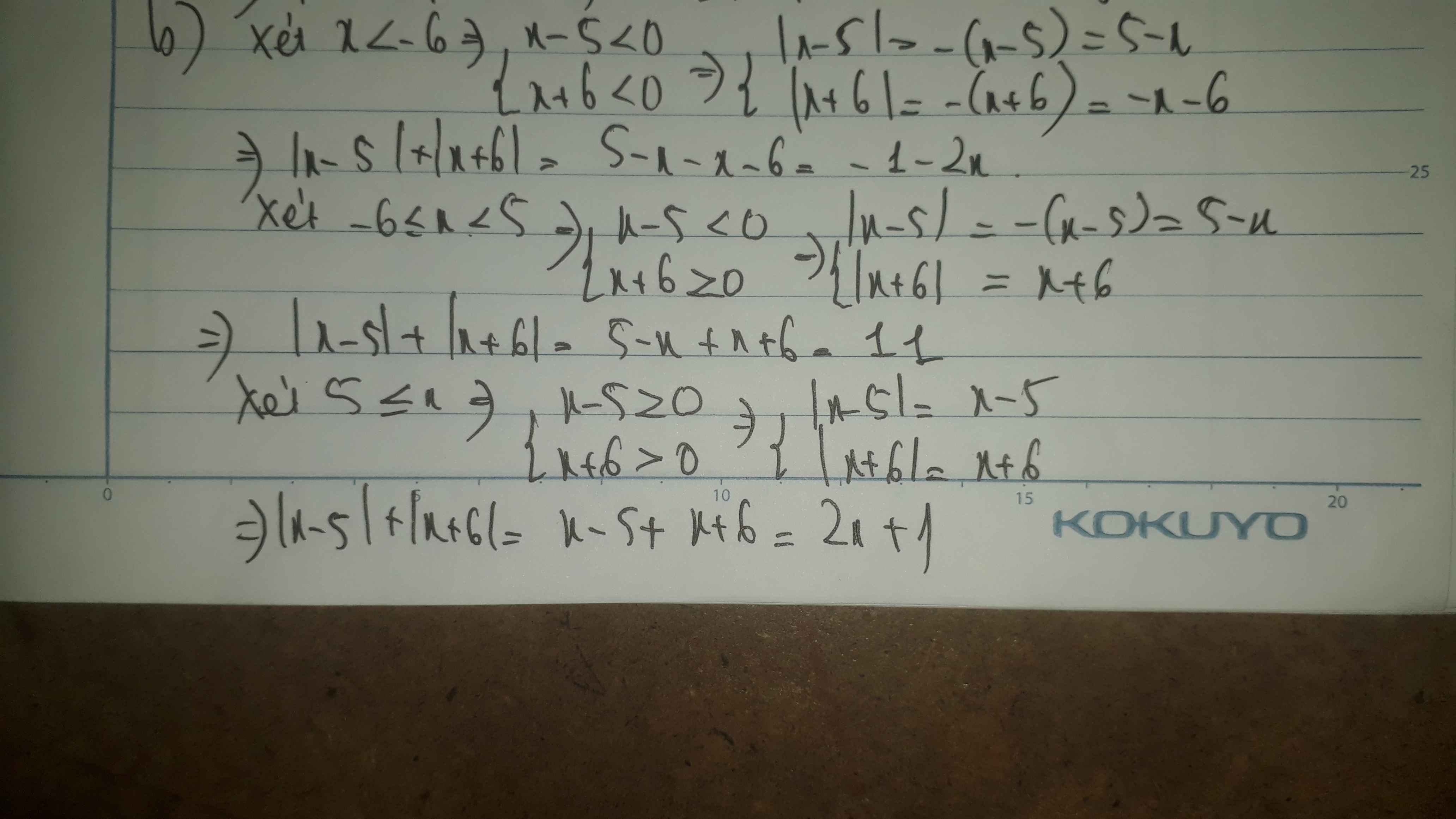Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau: A = | x - 4 | - x + 1 với x < 4

Những câu hỏi liên quan
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau: A = | x - 4 | - x + 1 với x < 4
Ta có: x < 4 ⇒ | x - 4 | = 4 - x
Khi đó ta có: A = | x - 4 | - x + 1 = 4 - x - x + 1 = 5 - 2x.
Vậy A = 5 - 2x
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau: A = 3x + 2 + | 5x | với x > 0
Với x > 0 ⇒ | 5x | = 5x
Khi đó ta có: A = 3x + 2 + | 5x | = 3x + 2 + 5x = 8x + 2
Vậy A = 8x + 2.
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau: A = | 4x | - 2x + 12 với x < 0.
Ta có: x < 0 ⇒ | 4x | = - 4x
Khi đó ta có: A = | 4x | - 2x + 12 = - 4x - 2x + 12 = 12 - 6x
Vậy A = 12 - 6x.
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau: A = 3x + 2 + | 5x | với x > 0.
Với x > 0 ⇒ | 5x | = 5x
Khi đó ta có: A = 3x + 2 + | 5x | = 3x + 2 + 5x = 8x + 2
Vậy A = 8x + 2.
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau: A = | 4x | - 2x + 12 với x < 0.
Ta có: x < 0 ⇒ | 4x | = - 4x
Khi đó ta có: A = | 4x | - 2x + 12 = - 4x - 2x + 12 = 12 - 6x
Vậy A = 12 - 6x.
Đúng 0
Bình luận (0)
Bỏ dấu gia trị tuyệt đối và rút gọn biểu thức sau: A=5x+4-/x-8/ với x<8
Với `x < 8 <=>x-8 < 0`
`=>|x-8|=8-x`
Khi đó `A` có dạng:
`A=5x+4-(8-x)`
`A=5x+4-8+x`
`A=6x-4`
Đúng 6
Bình luận (20)
Ta có: `|x - 8| = 8 - x ∀ x < 8`.
Với `x < 8` thì:
`<=> 5x + 4 - 8 + x`.
`<=> 6x - 4`.
Đúng 5
Bình luận (0)
Có : x < 8
=> x - 8 < 0
Có : A = 5x+4-|x-8|
=> A = 5x + 4 + ( x - 8 ) { vì x - 8 < 0 }
=> A = 5x + 4 + x - 8
=> A = 6x - 4
Đúng 2
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức sau: A = | x - 1 | + 3 - x khi x ≥ 1.
Khi x ≥ 1 ta có x - 1 ≥ 0 nên | x - 1 | = x - 1
Do đó A = | x - 1 | + 3 - x = x - 1 + 3 - x = 2.
Đúng 0
Bình luận (0)
Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức: C = |x - 4| - 2x + 12 khi x > 5
- Khi x > 5 ta có x - 4 > 1 (trừ hai vế cho 4) hay x - 4 > 0 nên |x - 4| = x - 4
Vậy C = x - 4 - 2x + 12 = -x + 8
Đúng 0
Bình luận (0)
bỏ dấu giá trị tuyệt đối rồi rút gọn các biểu thức sau:a,|2x-4|+|x-3|;b, |x-5|+|x+6|
a. \(\left|2x-4\right|+\left|x-3\right|\)
Với \(x< 2\), biểu thức trở thành
\(-\left(2x-4\right)-\left(x-3\right)\)
\(=-2x+4-x+3\)
\(=-3x+7\)
Với \(2\le x< 3\), biểu thức trở thành
\(\left(2x-4\right)-\left(x-3\right)\)
\(=2x-4-x+3\)
\(=x-1\)
Với \(x\ge3\), biểu thức trở thành
\(\left(2x-4\right)+\left(x-3\right)\)
\(=2x-4+x-3\)
\(=3x-7\)
b. \(\left|x-5\right|+\left|x+6\right|\)
Với \(x< -6\), biểu thức trở thành
\(-\left(x-5\right)-\left(x+6\right)\)
\(=-x+5-x-6\)
\(=-2x-1\)
Với \(-6\le x< 5\), biểu thức trở thành
\(-\left(x-5\right)+\left(x+6\right)\)
\(=-x+5+x+6\)
\(=11\)
Với \(x\ge5\), biểu thức trở thành
\(\left(x-5\right)+\left(x+6\right)\)
\(=x-5+x+6\)
\(=2x+1\)
Đúng 0
Bình luận (0)