Để tính ∫ xln ( 2 + x ) . dx theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
Những câu hỏi liên quan
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x ln ( 1 - x ) d x
x 2 2 ln 1 - x - 1 2 ln 1 - x - 1 4 1 + x 2 + C
Đúng 0
Bình luận (0)
Để tính
∫
x
ln
(
2
+
x
)
d
x
theo phương pháp tính nguyên hàm từng phần, ta đặt: A.
u
v
d
v
ln
2...
Đọc tiếp
Để tính ∫ x ln ( 2 + x ) d x theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
Chọn B.
Chú ý: “ Nhất log, nhì đa, tam lượng, tứ mũ”.
Đúng 0
Bình luận (0)
Để tính
∫
x
2
.
cos
x
.
d
x
theo phương pháp tính nguyên hàm từng phần, ta đặt: A.
u
x
d
v
x
cos
x
d...
Đọc tiếp
Để tính ∫ x 2 . cos x . d x theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = x d v = x cos x d x
B. u = x 2 d v = cos x d x
C. u = cos x d v = x 2 d x
D. u = x 2 cos x d v = d x
Chọn B.
Chú ý: “ Nhất log, nhì đa, tam lượng, tứ mũ”.
Đúng 0
Bình luận (0)
Tính nguyên hàm \(\int xln\left(x+1\right)dx\)
\(\left\{{}\begin{matrix}u=ln\left(x+1\right)\\dv=xdx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x+1}\\v=\dfrac{1}{2}x^2\end{matrix}\right.\)
\(\Rightarrow\int xln\left(x+1\right)dx=\dfrac{1}{2}x^2.ln\left(x+1\right)-\dfrac{1}{2}\int\dfrac{x^2}{x+1}dx\)
\(\int\dfrac{x^2dx}{x+1}=\int\left(x-1\right)dx+\int\dfrac{dx}{x+1}\)
P/s: Tất cả đã về dạng cơ bản, bạn tự làm nốt ạ
Đúng 3
Bình luận (0)
Cho P(x) là đa thức của x. Từ Ví dụ 9, hãy lập bảng theo mẫu dưới đây rồi điền u và dv thích hợp vào chỗ trống theo phương pháp nguyên phân hàm từng phần.
∫ P(x)
e
x
dx
∫ P(x)cosxdx
∫ P(x)lnxdx
P(x)
e
x
dx
Đọc tiếp
Cho P(x) là đa thức của x. Từ Ví dụ 9, hãy lập bảng theo mẫu dưới đây rồi điền u và dv thích hợp vào chỗ trống theo phương pháp nguyên phân hàm từng phần.
| ∫ P(x) e x dx | ∫ P(x)cosxdx | ∫ P(x)lnxdx |
| P(x) | ||
| e x dx |
| ∫ P(x) e x dx | ∫ P(x)cosxdx | ∫ P(x)lnxdx |
| P(x) | P(x) | P(x)lnx |
| e x dx | cosxdx | dx |
Đúng 0
Bình luận (0)
Hãy tính ∫ x + 1 e x d x bằng phương pháp tính nguyên hàm từng phần.
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính:
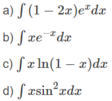
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x sin 2 x d x
x 2 4 - x 4 sin 2 x - 1 8 c o s 2 x + C
HD: Đặt u = x, dv = sin 2 x dx
Đúng 0
Bình luận (0)
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính :
a) \(\int x\ln\left(1+x\right)dx\)
b) \(\int\left(x^2+2x-1\right)e^xdx\)
c) \(\int x\sin\left(2x+1\right)dx\)
d) \(\int\left(1-x\right)\cos xdx\)
a) Áp dụng phương pháp tìm nguyên hàm từng phần:
Đặt u= ln(1+x)
dv= xdx
=> ,
Ta có: ∫xln(1+x)dx =
=
b) Cách 1: Tìm nguyên hàm từng phần hai lần:
Đặt u= (x2+2x -1) và dv=exdx
Suy ra du = (2x+2)dx, v = ex
. Khi đó:
∫(x2+2x - 1)exdx = (x2+2x - 1)exdx - ∫(2x+2)exdx
Đặt : u=2x+2; dv=exdx
=> du = 2dx ;v=ex
Khi đó:∫(2x+2)exdx = (2x+2)ex - 2∫exdx = ex(2x+2) – 2ex+C
Vậy
∫(x2+2x+1)exdx = ex(x2-1) + C
Cách 2: HD: Ta tìm ∫(x2-1)exdx. Đặt u = x2-1 và dv=exdx.
Đáp số : ex(x2-1) + C
c) Đáp số:
HD: Đặt u=x ; dv = sin(2x+1)dx
d) Đáp số : (1-x)sinx - cosx +C.
HD: Đặt u = 1 - x ;dv = cosxdx
Đúng 0
Bình luận (0)