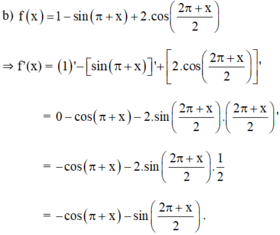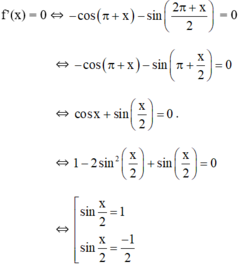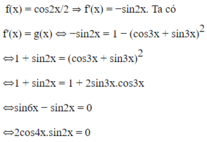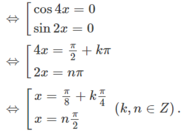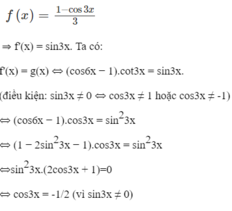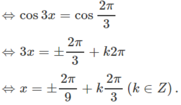Giải phương trình f ' x = 0 , biết rằng: f x = 3 x + 60 x - 64 x 3 + 5

Những câu hỏi liên quan
Giải phương trình f'(x) = 0, biết rằng f ( x ) = 3 x + 60 x - 64 x 3 + 5
Giải phương trình f(x) 0, biết rằng
f
(
x
)
sin
3
x
3
+
cos
x
-
3
sin
x
+
cos
3...
Đọc tiếp
Giải phương trình f'(x) = 0, biết rằng f ( x ) = sin 3 x 3 + cos x - 3 sin x + cos 3 x 3
Giải phương trình f(x) 0, biết rằng:
f
x
1
-
sin
π
+
x
+
2
cos
2
π
+
x
2
Đọc tiếp
Giải phương trình f'(x) = 0, biết rằng: f x = 1 - sin π + x + 2 cos 2 π + x 2
Giải phương trình f′(x) g(x), biết rằng
f
(
x
)
1
2
cos
2
x
,
g
(
x
)
1
-
cos
3
x
+
sin
3...
Đọc tiếp
Giải phương trình f′(x) = g(x), biết rằng f ( x ) = 1 2 cos 2 x , g ( x ) = 1 - cos 3 x + sin 3 x 2
Giải phương trình f′(x) g(x), biết rằng
f
(
x
)
1
-
cos
3
x
3
;
g
(
x
)
cos
6
x
-...
Đọc tiếp
Giải phương trình f′(x) = g(x), biết rằng f ( x ) = 1 - cos 3 x 3 ; g ( x ) = cos 6 x - 1 c o t 3 x
Giải phương trình f′(x) g(x), biết rằng
f
(
x
)
1
2
sin
2
x
+
5
cos
x
,
g
(
x
)
3
sin
2
x
+
3
1
+...
Đọc tiếp
Giải phương trình f′(x) = g(x), biết rằng f ( x ) = 1 2 sin 2 x + 5 cos x , g ( x ) = 3 sin 2 x + 3 1 + tan 2 x
f(x) = sin2x/2 + 5cosx ⇒ f′(x) = cos2x − 5sinx. Ta có
f′(x) = g(x)
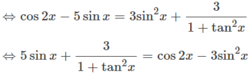

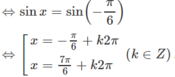
Đúng 0
Bình luận (0)
cho hàm số \(f\left(x\right)=x^3-3x^2+2\)
a, giải bất phương trình \(f'\left(x\right)\le0\)
b, giải phương trình \(f'=\left(x^2-3x+2\right)=0\)
c, đặt \(g\left(x\right)=f\left(1-2x\right)+x^2-x+2022\) giải bất phương trình\(g'\left(x\right)\ge0\)
\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Đúng 2
Bình luận (0)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$
Đúng 1
Bình luận (0)
Giải phương trình \(f'\left(x\right)=0\) biết rằng :
\(f\left(x\right)=3x+\dfrac{60}{x}-\dfrac{64}{x^3}+5\)
Giải phương trình \(f'\left(x\right)=0\) biết rằng :
a) \(f\left(x\right)=3x+\dfrac{60}{x}-\dfrac{64}{x^3}+5\)
b) \(f\left(x\right)=\dfrac{\sin3x}{3}+\cos x-\sqrt{3}\left(\sin x+\dfrac{\cos3x}{3}\right)\)
Giải các bất phương trình
f
(
x
)
0
v
ớ
i
f
(
x
)
1
7
x
7
-
9
4
x
4
+
8
x
-
3
Đọc tiếp
Giải các bất phương trình f ' ( x ) > 0 v ớ i f ( x ) = 1 7 x 7 - 9 4 x 4 + 8 x - 3