Giải các phương trình sau: | - 5x | - 16 = 3x

Những câu hỏi liên quan
Giải các phương trình sau: | - 5x | - 16 = 3x
Ta có: | - 5x | - 16 = 3x
+ Với x ≥ 0, phương trình tương đương: 5x - 16 = 3x ⇔ 2x = 16 ⇔ x = 8
Thỏa mãn điều kiện x ≥ 0
+ Với x < 0, phương trình tương đương: - 5x - 16 = 3x ⇔ 8x = - 16 ⇔ x = - 2
Thỏa mãn điều kiện x < 0
Vậy phương trình đã cho có tập nghiệm là S = { - 2;8 }
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
12
x
+
4
21
−
x
−
3
3
3
x
−
2
7
;
b)
5
x
−...
Đọc tiếp
Giải các phương trình sau:
a) 12 x + 4 21 − x − 3 3 = 3 x − 2 7 ;
b) 5 x − 1 2 − 1 6 − 2 x = 9 x − 8 12 .
Giải các phương trình sau:a)
4
x
−
5
x
+
7
; b)
10
x
−
12
−
3
x
6
+
x
;
c)
5
x
−
4
3
2
+
3
x...
Đọc tiếp
Giải các phương trình sau:
a) 4 x − 5 = x + 7 ; b) 10 x − 12 − 3 x = 6 + x ;
c) 5 x − 4 3 = 2 + 3 x 2 d) 7 x − 1 6 + 2 x = 16 − x 5 .
giải bất phương trình sau :
|-5x|=3x-16
\(|-5x|=3x-16\)
\(TH1:-5x=3x-16\Leftrightarrow-8x=-16\Leftrightarrow x=2\)
\(TH2:-5x=-3x+16\Leftrightarrow-2x=16\Leftrightarrow x=-8\)
Đúng 0
Bình luận (0)
Giải các phương trình sau:
a
)
5
x
-
3
2
4
x
-
7
2
*
b
)
96
x
2
-
16
+
6
2...
Đọc tiếp
Giải các phương trình sau:
a ) 5 x - 3 2 = 4 x - 7 2 * b ) 96 x 2 - 16 + 6 = 2 x - 1 x + 4 + 3 x - 1 x - 4 c ) 1 - x 2 x 2 - 4 x - 1 4 x - 4 = x - 1 2 x x - 2 - 1 2 x
a) (*) ⇔ (5x – 3)2 – (4x – 7)2 = 0
⇔ (5x – 3 + 4x – 7)(5x – 3 – 4x + 7) = 0
⇔ (9x – 10)(x + 4) = 0 ⇔ 9x – 10 = 0 hoặc x + 4 = 0
⇔ x = 10/9 hoặc x = -4
Tập nghiệm : S = { 10/9 ; -4}
b) ĐKXĐ: (x + 4)(x – 4) ≠ 0 ⇔ x + 4 ≠ 0 và x – 4 ≠ 0 ⇔ x ≠ ⇔ 4
Ta có: x2 – 16 = (x + 4)(x – 4) ≠ 0
Quy đồng và khử mẫu, ta được:
96 + 6(x2 – 16) = (2x – 1)(x – 4) + (3x – 1)(x + 4)
⇔ 96 + 6x2 – 96 = 2x2 – 8x – x + 4 + 3x2 + 12x – x – 4
⇔ x2 – 2x = 0 ⇔ x(x – 2) = 0
⇔ x = 0 hoặc x – 2 = 0
⇔ x = 0 hoặc x = 2 (thỏa mãn ĐKXĐ)
Tập nghiệm: S = {0;2}
c) ĐKXĐ: x ≠ 0; x – 1 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ 0; x ≠ 1 và x ≠ 2
MTC: 4x(x – 2)(x – 1)
Quy đồng và khử mẫu, ta được:
2(1 – x)(x – 1) – x(x – 2) = 2(x – 1)2 – 2(x – 1)(x – 2)
⇔ -2x2 + 4x – 2 – x2 + 2x = 2x2 – 4x + 2 – 2x2 + 6x – 4
⇔ 3x2 – 4x = 0 ⇔ x(3x – 4) = 0 ⇔ x = 0 hoặc x = 4/3
(x = 0 không thỏa mãn ĐKXĐ)
Tập nghiệm: S = {4/3}
Đúng 0
Bình luận (0)
Giải phương trình: |-5x| - 16 = 3x
|-5x| - 16 = 3x (4)
Ta có: |-5x| = -5x khi -5x ≥ 0 hay x ≤ 0.
|-5x| = -(-5x) = 5x khi -5x < 0 hay x > 0.
Vậy phương trình (4) tương đương với:
+ -5x – 16 = 3x với điều kiện x ≤ 0.
-5x – 16 = 3x ⇔ -5x – 3x = 16 ⇔ -8x = 16 ⇔ x = -2.
Giá trị x = -2 thỏa mãn điều kiện x ≤ 0 nên là nghiệm của (4).
+ 5x – 16 = 3x với điều kiện x > 0.
5x – 16 = 3x ⇔ 5x – 3x = 16 ⇔ 2x = 16 ⇔ x = 8
Giá trị x = 8 thỏa mãn điều kiện x > 0 nên là nghiệm của (4).
Vậy phương trình (4) có nghiệm x = -2 và x = 8.
Đúng 0
Bình luận (0)
Giải các phương trình sau:
1) \(\sqrt{2x+4}-2\sqrt{2-x}=\dfrac{12x-8}{\sqrt{9x^2+16}}.\)
2) \(\sqrt{3x^2-7x+3}-\sqrt{x^2-2}=\sqrt{3x^2-5x-1}-\sqrt{x^2-3x+4}.\)
Giải các phương trình sau: 5x + 16 = 0.
5x + 16 =0
⇔ 5x = -16
⇔ 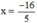 .
.
Vậy phương trình có nghiệm 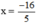 .
.
Đúng 0
Bình luận (0)
Giải các phương trình sau: (2 – 3x)(x + 11) = (3x – 2)(2 – 5x)
(2 – 3x)(x + 11) = (3x – 2)(2 – 5x)
⇔ (2 – 3x)(x + 11) – (3x – 2)(2 – 5x) = 0
⇔ (2 – 3x)(x + 11) + (2 – 3x)(2 – 5x) = 0
⇔ (2 – 3x)[(x + 11) + (2 – 5x)] = 0
⇔ (2 – 3x)(x + 11 + 2 – 5x) = 0
⇔ (2 – 3x)(13 – 4x) = 0 ⇔ 2 – 3x = 0 hoặc 13 – 4x = 0
2 – 3x = 0 ⇔ x = 2/3
13 – 4x = 0 ⇔ x = 13/4
Vậy phương trình có nghiệm x = 2/3 hoặc x = 13/4
Đúng 0
Bình luận (0)





