Gọi I là giao điểm của ba đường phân giác của tam giác. Kết luận nào sau đây là đúng?
A. I cách đều 3 cạnh của tam giác
B. I cách đều ba đỉnh của tam giác
C. I là trọng tâm của tam giác
D. I là trực tâm của tam giác
CÂU 1: GỌI ILAF GIAO ĐIỂM CỦA 3 ĐƯỜNG THANGWR TRUNG TRỰC CỦA TAM GIÁC.KẾT LUẬN NÀO ĐÚNG
A)I CÁCH ĐỀU 3 CẠNH CỦA TAM GIÁC B)I CÁCH ĐỀU 3 ĐỈNH CỦA TAM GIÁC
C)I LÀ TRỌNG TÂM CỦA TAM GIÁC D)I LÀ TRỰC TÂM CỦA TAM GIÁC
CÂU 2; TAM GIÁC MNP CÓ <P= 74 ĐỘ , K LÀ GIAO ĐIỂM CỦA 3 ĐƯỜNG PHÂN GIÁC . GÓC MKN=?
A 106 ĐỌ B 120 ĐỘ C 127 ĐỘ D 143 ĐÔ
CÂU 3 CHO TAM GIÁC ABC M TĐ BC G LÀ TRỌNG TÂM VÀ AM=12CM .AG=?
A8CM B6CM C4CM D3CM
Câu 1: I là giao điểm của 3 đường trung trực nên nó cách đều 3 đỉnh của tam giác đó.
Đáp án: B)
Câu 2: Đáp án: C) 1270
Câu 3: \(AG=\frac{2}{3}AM=\frac{2}{3}.12=8\left(cm\right)\)
Đáp án: A)
cho tam giác ABC cân tại .gọi G là trọng tâm,I là điểm nằm trong tam giác và cách đều 3 cạnh của tam giác đó.Chứng minh ba điểm A,G,I thẳng hàng
Xét tam giác ABC cân tại A có:
G là trọng tâm
=> G là giao của 3 đường trung tuyến
=>AG là đường trung tuyến
Mà tam giác ABC cân tại A
=>AG cũng là đường trung trực
Mà AI là đường trung trực(do I cách đều 3 điểm)
=>AG trùng AI(Tiên đề Ơ clit)
=>A,G,I thẳng hàng
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà 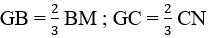
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của
Vì G, I cùng thuộc tia phân giác của 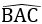
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
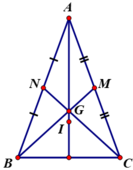
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà 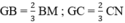 (Tính chất trọng tâm của tam giác)
(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
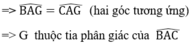
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của 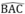
Vì G, I cùng thuộc tia phân giác của 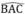 nên A, G, I thẳng hàng
nên A, G, I thẳng hàng
cho tam giác abc, i là điểm nằm trong tam giác và i cách đều hai cạnh ab và ac phát biểu nào là đúng
a/ ai, bi là các tia phân giác của góc a, b
b/ i là giao điểm của ba đường phân giác
c/ai là trung tuyến của bc
d/cả ba đề sai
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
Gọi giao điểm của BG với AC là M ;
CG với AB là N
Vì G là trọng tâm của \(\Delta ABC\)
nên BM, CN, là trung tuyến
Mặt khác \(\Delta ABC\) cân tại A
Nên BM = CN
Ta có : \(GB=\frac{1}{2}BM;GC=\frac{2}{3}CN\) (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó : \(\Delta AGB=\Delta AGC\left(c.c.c\right)\)
\(\Rightarrow\widehat{BAG}=\widehat{CAG}\Rightarrow G\) thuộc phân giác của \(\widehat{BAC}\)
Mà \(\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\Rightarrow I\) thuộc phân giác của \(\widehat{BAC}\)
Vì G, I cùng thuộc phân giác của \(\widehat{BAC}\) nên A, G, I thẳng hàng
Chúc bạn học tốt !!!
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
Giải
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà \(GB=\frac{2}{3}BM;GC=\frac{2}{3}CN\)(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
\(\Rightarrow\widehat{BAG}=\widehat{CAG}\)( hai góc tương ứng )
\(\Rightarrow\)G là trọng tâm của \(\widehat{BAC}\)
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của \(\widehat{BAC}\)
Vì G, I cùng thuộc tia phân giác của \(\widehat{BAC}\)nên A, G, I thẳng hàng
Cho tam giác ABC cân Tại A . Gọi G là Trọng Tâm I Là Điểm Nằm Trong Tam Giác Và Cách Đều Ba Cạnh Của Tam Giác Đó . Chứng Minh Ba Điểm A , G , I Thẳng Hàng .
Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = BM; GC = CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> => G thuộc phân giác của
Mà ∆ABI = ∆ACI (c.c.c)
=> => I thuộc phân giác của
Vì G, I cùng thuộc phân giác của nên A, G, I thẳng hàng
Vì G là trọng tâm của tam giác ABC trên D thuộc đường trung tuyến AM (1)
Vì I là giao điểm các phân giác của tam giác ABC nên AI là tia phân giác của góc A mà trong tam giác cân phân giác của góc ở đỉnh của tam giác cũng là trung tuyến do đó I thuộc trực tuyến AM(2)
Từ (1) và (2 )suy ra 3 điểm A,I,G thẳng hàng
G là trọng tâm của ΔABCΔABC nên G thuộc đường trung tuyến AM (1)
Trong tam giác cân, đường trung phân giác của góc ở đỉnh đồng thời là đường trung tuyến nên I cũng thuộc đường trung tuyến AM. (2)
Từ (1) và (2) suy ra A, G, I thẳng hàng.
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó . Chứng minh ba điểm A,G,I thẳng hàng