Tuc la a+ b+c=12abc va a+b+c=1/a^2 +1/b^2 +1/c^2 chu gi? 

a) Áp dụng Cauchy Schwars ta có:

\(M=\frac{a^2}{a+1}+\frac{b^2}{b+1}+\frac{c^2}{c+1}\ge\frac{\left(a+b+c\right)^2}{a+b+c+3}=\frac{9}{6}=\frac{3}{2}\)

Dấu "=" xảy ra khi: a = b = c = 1

b) \(N=\frac{1}{a}+\frac{4}{b+1}+\frac{9}{c+2}\ge\frac{\left(1+2+3\right)^2}{a+b+c+3}=\frac{36}{6}=6\)

Dấu "=" xảy ra khi: x=y=1

c) \(P=\frac{a^2}{a+b}+\frac{b^2}{b+c}+\frac{c^2}{c+a}\ge\frac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}=\frac{9}{2.3}=\frac{3}{2}\)

Dấu "=" xảy ra khi: x=y=1

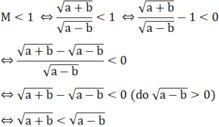
<=> a+b < a-b

<=> b < 0

Vô lí do a > b > 0

Vậy không tồn tại a, b sao cho M < 1

Do a+b+c= 0

<=> a+b= -c 

=> (a+b)²= c² 

Tương tự: (c+a)²= b², (c+b)²= a²   

Ta có: \(A=\frac{1}{b^2+c^2-a^2}+\frac{1}{c^2+a^2-b^2}+\frac{1}{a^2+b^2-c^2}\)

\(=\frac{1}{b^2+c^2-\left(b+c\right)^2}+\frac{1}{c^2+a^2-\left(c+a\right)^2}+\frac{1}{a^2+b^2-\left(a+b\right)^2}\)

\(=\frac{1}{-2bc}+\frac{1}{-2ca}+\frac{1}{-2ab}\)

\(=\frac{a+b+c}{-2abc}=0\)