Cho hàm số f(x) xác định bởi f ( x ) = x 2 + 1 - x x ( x ≠ 0 ) 0 ( x = 0 ) . Giá trị f’(0) bằng:
A. 0
B. 1
C. 1/2.
D. Không tồn tại.
Những câu hỏi liên quan
Cho các hàm số y = f(x) xác định bởi: f(-3) = -2; f(-1) = -6; f(1,5) = 4; f(2) = 3; f(4) = 1,5
a) Cho biết tập xác định D của hàm số này.
b) Hàm số y = f(x) có thể được cho bởi công thức nào ?
Cho hàm số f(x) xác định trên R bởi
f
(
x
)
x
2
. Giá trị f (0) bằng A. 0 B. 2 C. 1 D. không tồn tại
Đọc tiếp
Cho hàm số f(x) xác định trên R bởi f ( x ) = x 2 . Giá trị f ' (0) bằng
A. 0
B. 2
C. 1
D. không tồn tại
Chọn D
Ta có : f ' x = 1 2 x 2 . ( x 2 ) ' = x x 2
-> f '(x) không xác định tại x = 0
-> f ' (0) không có đạo hàm tại x= 0
Đúng 0
Bình luận (0)
Cho hàm số f(x) xác định trên R bởi f(x)= 2 x 2 + 1 . Giá trị f ' (-1) bằng:
A. 2
B. 6
C. - 4
D. 3
Chọn C
Ta có : .f ' (x)=4x ⇒ f ' (-1)=-4
Đúng 0
Bình luận (0)
Cho hàm số f(x) xác định trên R bởi f(x) = 2x2 + 1. Giá trị f’(-1) bằng:
A. 2.
B. 6.
C. -4.
D. 3.
Chọn C.
Ta có : f’(x) = 4x ⇒ f’(-1) = -4.
Đúng 0
Bình luận (0)
Cho hàm số f(x) xác định trên R bởi f ( x ) = 2 x 2 + 1 . Giá trị f'(-1) bằng:
A. 2
B. 6
C. -4
D. 3
Cho hàm số f(x) xác định bởi 
. Giá trị f’(0) bằng
A. 0
B. 2
C. 1
D. Không tồn tại.
Chọn D.
Ta có :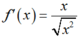 
⇒ f’(x) không xác định tại x = 0
⇒ f’(0) không có đạo hàm tại x = 0.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) xác định trên tập số thực và có đạo hàm f(x). Đồ thị hàm số y f(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) f(4). - f(3). Giá trị nhỏ nhất của hàm số y f(x) trên đoạn [0;4] là A. f(1) B. f(0) C. f(2) D. f(4)
Đọc tiếp
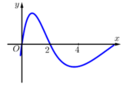
Cho hàm số y = f(x) xác định trên tập số thực và có đạo hàm f'(x). Đồ thị hàm số y = f'(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) = f(4). - f(3). Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0;4] là
A. f(1)
B. f(0)
C. f(2)
D. f(4)
Chọn D
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
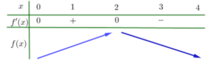
Từ bảng biến thiên, ta có nhận xét sau: 
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
Đúng 0
Bình luận (0)
Cho hàm số xác định bởi
y
f
(
x
)
40
x
+
20
, Với giá tri nào của x thì
f
(
x
)
300
? A. x 7 B. x 70 C. x 17 D. x 140
Đọc tiếp
Cho hàm số xác định bởi y = f ( x ) = 40 x + 20 , Với giá tri nào của x thì f ( x ) = 300 ?
A. x = 7
B. x = 70
C. x = 17
D. x = 140
Cho hàm số xác định bởi
y
f
(
x
)
−
4
x
−
2020
. Với giá tri nào của x thì
f
(
x
)
−
2040
? A. x 5 B. x 50 C. x 1015 D. x 80
Đọc tiếp
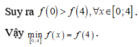
Cho hàm số xác định bởi y = f ( x ) = − 4 x − 2020 . Với giá tri nào của x thì f ( x ) = − 2040 ?
A. x = 5
B. x = 50
C. x = 1015
D. x = 80
