∗ Dòng điện cảm ứng

Dòng điện cảm ứng là dòng điện xuất hiện trong một khung dây dẫn kín trong từ trường khi từ thông gửi qua khung dây bị biến thiên và có tác dụng chống lại sự biến thiên của từ thông sinh ra nó.

∗ Hiện tượng cảm ứng điện từ

- Là hiện tượng xuất hiện dòng điện cảm ứng trong một mạch kín khi từ thông qua mạch biến thiên.

- Khi có sự biến thiên từ thông qua diện tích giới hạn bởi một mạch điện kín thì trong mạch xuất hiện dòng điện cảm ứng.

- Hiện tượng cảm ứng điện từ chỉ tồn tại trong khoảng thời gian từ thông qua mạch kín biến thiên.

∗ Từ trường cảm ứng

- Từ trường cảm ứng là từ trường sinh ra bởi dòng điện cảm ứng và có tác dụng chống lại nguyên nhân sinh ra nó. Tức là chống lại sự biến thiên của từ thông gửi qua mạch kín mang dòng điện cảm ứng.

- Nếu sự biến thiên của từ thông này là do sự chuyển động của khung dây thì từ trường cảm ứng sẽ sinh ra lực từ chống lại sự chuyển động đó.

Từ trường là một dạng vật chất tồn tại trong không gian mà biểu hiện cụ thể là sự tác dụng lực từ lên một dòng điện hay một nam châm đặt trong nó.

1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.

2. -Có 3 trường hợp bằng nhau của 2 tam giác:

+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).

+Trường hợp 2: cạnh-góc-cạnh(c.g.c).

+Trường hợp 3: góc-cạnh-góc(g.c.g)

3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông

4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau

-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau

+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân

- Cách chứng minh 1 tam giác là tam giác cân:

+ Chứng minh tam giác có 2 cạnh bằng nhau

+ Chứng minh tam giác có 2 góc bằng nhau

+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)

5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau

- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ

+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều

+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều

- Cách chứng minh 1 tam giác là tam giác đều:

+Chứng minh tam giác có 3 cạnh bằng nhau

+Chứng minh tam giác có 3 góc bằng nhau

+Chứng minh tam giác có 2 góc có 60 độ

+Chứng minh tam giác cân có 1 góc có 60 độ

6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông

- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông

1.- Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.

2. -Có 3 trường hợp bằng nhau của 2 tam giác:

+Trường hợp 1: cạnh-cạnh-cạnh(c.c.c).

+Trường hợp 2: cạnh-góc-cạnh(c.g.c).

+Trường hợp 3: góc-cạnh-góc(g.c.g)

3. -Đối với tam giác vuông cũng có các trường hợp như câu trên và trường hợp bằng nhau về cạnh huyền và cạnh góc vuông

4.- Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau

-Tính chất:+Trong 1 tam giác cân, 2 góc ở đáy bằng nhau

+Nếu 1 tam giác có 2 góc bằng nhau thì tam giác đó là tam giác cân

- Cách chứng minh 1 tam giác là tam giác cân:

+ Chứng minh tam giác có 2 cạnh bằng nhau

+ Chứng minh tam giác có 2 góc bằng nhau

+ Chứng minh tam giác có đường trung tuyến vừa là đường cao hoặc phân giác( và ngược lại)

5. - Định nghĩa: Tam giác đều là tam giác có 3 cạnh bằng nhau

- Tính chất:+Trong 1 tam giác đều, mỗi góc bằng 60 độ

+Nếu 1 tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều

+Nếu 1 tam giác cân có 1 góc bằng 60 độ thì tam giác đó là tam giác đều

- Cách chứng minh 1 tam giác là tam giác đều:

+Chứng minh tam giác có 3 cạnh bằng nhau

+Chứng minh tam giác có 3 góc bằng nhau

+Chứng minh tam giác có 2 góc có 60 độ

+Chứng minh tam giác cân có 1 góc có 60 độ

6. -Định lí Py-ta-go: Trong 1 tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông

- Định lí Py-ta-go đảo: Nếu 1 tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông

Dòng điện cảm ứng là dòng điện xuất hiện trong mạch kín khi từ thông qua mạch biến thiên .

Hiện tượng cảm ứng điện từ là hiện tượng xuất hiện dòng điện cảm ứng trong mạch kín khi từ thông qua mạch biến thiên .

Từ trường cảm ứng là từ trường xuất hiện xung quanh dây dẫn khi xảy ra hiện tượng cảm ứng từ trường .

Lực từ

• Vecto lực từ F là lực tác dụng nên một dòng điện hay một phần tử dòng điện đặt trong từ trường.

• Vecto lực từ F tác dụng nên phần tử dòng điện I. 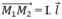 khi đặt trong từ trường đều, tại đó có cảm ứng từ B ⃗ được xác định:

- Điểm đặt: Tại trung điểm của M1M2

- Phương: vuông góc với l và B.

- Chiều: tuân theo quy tắc bàn tay trái “để bàn tay trái sao cho B hướng vào lòng bàn ta, chiều từ cổ tay đến ngón giữa là chiều dòng điện 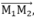 khi đó chiều ngón cái choãi ra chỉ chiều của F”.

- Độ lớn: F = I.B.l.sinα (trong đó α là góc hợp bởi B và l)

Cảm ứng từ.

Vectơ cảm ứng từ đặc trưng cho từ trường tại một điểm – ký hiệu B được xác định bởi

- Hướng: trùng với hướng của từ trường tại điểm đó.

- Độ lớn: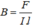 

(Trong đó F: độ lớn của lực từ tác dụng nên phần tử dòng điện có độ dài l, cường độ dòng điện I đặt vuông góc với hướng của từ trường tại điểm đó)

- Đơn vị cảm ứng: Tesla (T) (1T = 1N/(A.m))

- Tam giác đều là tam giác có ba cạnh bằng nhau.

- Tính chất: Trong một tam giác đều, mỗi góc bằng 60o

- Các cách chứng minh một tam giác là tam giác đều:

   • Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

   • Nếu một tam giác cân có một góc bằng 60o thì tam giác đó là tam giác đều.