2. Hãy nêu cách tính diện tích xung quanh và thể tích của hình nón cụt.

Những câu hỏi liên quan
Hãy nêu cách tính diện tích xung quanh và thể tích của hình nón cụt.
Cách 1: Áp dụng công thức
- Với hình nón cụt có các bán kính các đáy là r1, r2, đường sinh l và chiều cao h thì :
Sxq= π(r1+ r2).l
V = 1/3πh(r12+ r22+ r1 r2)
Như vậy :
Diện tích xung quanh hình nón cụt thì bằng tích của số π với tổng hai bán kính và với đường sinh.
Thể tích của hình nón cụt thì bằng 1/3 tích của số π với đường cao h và tổng bình phương các bán kính cộng thêm tích của hai bán kính .
Cách 2: Vì hình nón cụt được cắt ra từ hình nón nên ta có thể tính
V(nón cụt )=V(nón lớn )-V(nón nhỏ )
S(xq nón cụt )=S(xq nón lớn )-S(xq nón nhỏ )
Đúng 0
Bình luận (0)
Cho hình nón cụt như hình vẽ Biết rằng bán kính của đáy nhỏ là r = 3cm, bán kính của đáy lớn là R = 6cm, độ dài AC = 4cm. Hãy tính diện tích xung quanh, diện tích toàn phần, và thể tích của hình nón cụt

Lời giải:
Diện tích xung quanh hình nón:
$\pi (r+R).l=\pi (6+3).4=36\pi$ (cm vuông)
Diện tích toàn phần:
$36\pi+\pi r^2+\pi R^2=36\pi +\pi.3^2+\pi. 6^2=81\pi$ (cm vuông)
Thể tích:
Chiều cao hình nón: $\sqrt{4^2-(6-3)^2}=\sqrt{7}$ (cm)
$\frac{1}{3}\pi (r^2+R^2+r.R)h=\frac{1}{3}\pi (3^2+6^2+3.6).\sqrt{7}=21\sqrt{7}\pi$ (cm khối)
Đúng 0
Bình luận (0)
Bài 3: Cho hình nón cụt như hình vẽ Biết rằng bán kính của đáy nhỏ là r= 3cm, bán kính của đáy lớn là R = 6cm, độ dài AB = 4cm. Hãy tính diện tích xung quanh, diện tích toàn phần, và thể tích của hình nón cụt
Bài 3: Cho hình nón cụt như hình vẽ Biết rằng bán kính của đáy nhỏ là r= 3cm, bán kính của đáy lớn là R = 6cm, độ dài AB = 4cm. Hãy tính diện tích xung quanh, diện tích toàn phần, và thể tích của hình nón cụt
Hình vẽ đâu bn.(không có hình thì mik ko bt AB là đường sinh hay chiều cao nhé. Nhưng thường thì AB là đường sinh)
(nếu đề bài AB là đường cao thì bn đăng lại nhé)
\(Sxq=\pi\left(r+R\right)l=\pi\left(3+6\right)4=36\pi\left(cm^2\right)\)
\(Stp=\pi\left(r+R\right)l+\pi\left(r^2+R^2\right)=36\pi+\pi\left(3^2+6^2\right)=36\pi+45\pi\)
\(=81\pi\left(cm^2\right)\)
có: \(h=\sqrt{l^2-\left(R-r\right)^2}=\sqrt{4^2-\left(6-3\right)^2}=\sqrt{7}cm\)
\(V=\dfrac{1}{3}\pi\left(r^2+R^2+rR\right).h\)\(=\dfrac{1}{3}\pi.\left(3^2+6^2+3.6\right).\sqrt{7}=21\sqrt{7}.\pi\left(cm^3\right)\)
Đúng 0
Bình luận (0)
Diện tích xung quanh, toàn phần và thể tích của hình trụ.
Diện tích xung quanh, toàn phần và thể tích của hình nón (cụt).
Diện tích xung quanh, toàn phần và thể tích của hình cầu.
tham khảo
Diện tích hình trụDiện tích hình trụ gồm có diện tích xung quanh và diện tích toàn phần.
Diện tích xung quanh hình trụDiện tích xung quanh hình trụ chỉ bao gồm diện tích mặt xung quanh, bao quanh hình trụ, không gồm diện tích hai đáy.Công thức tính diện tích xung quanh bằng chu vi đường tròn đáy nhân với chiều cao.
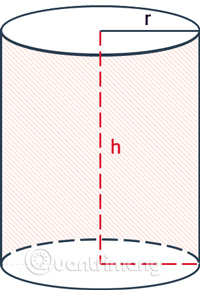 | Trong đó: Sxung quanh là diện tích xung quanh.r là bán kính hình trụ.h là chiều cao, khoảng cách giữa 2 đáy của hình trụ. |
Diện tích toàn phần được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích hai đáy tròn.
Công thức tính diện tích toàn phần bằng diện tích xung quanh cộng với diện tích của 2 đáy
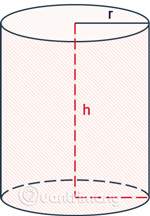 |
Đúng 1
Bình luận (2)
Cho hình thang vuông ABCD vuông tại A và B, biết cạnh AB = BC = 3cm, AD = 7cm. Tính diện tích xung quanh và thể tích hình nón cụt tạo thành khi quay hình thang quanh cạnh AB
1. Hãy phát biểu bằng lời:a) Công thức tính diện tích xung quanh của hình trụ.b) Công thức tính thể tích của hình trụ.c) Công thức tính diện tích xung quanh của hình nón.d) Công thức tính thể tích của hình nón.e) Công thức tính diện tích của mặt cầu.f) Công thức tính thể tích của hình cầu.
Đọc tiếp
1. Hãy phát biểu bằng lời:
a) Công thức tính diện tích xung quanh của hình trụ.
b) Công thức tính thể tích của hình trụ.
c) Công thức tính diện tích xung quanh của hình nón.
d) Công thức tính thể tích của hình nón.
e) Công thức tính diện tích của mặt cầu.
f) Công thức tính thể tích của hình cầu.
a) Diện tích xung quanh hình lăng trụ thì bằng chu vi đường tròn đáy nhân với chiều cao.
b) Thể tích hình trụ thì bằng tích của diện tích hình tròn đáy nhân với đường cao.
c) Diện tích xung quanh hình nón thì bằng 1/2 tích của chu vi đường tròn đáy với đường sinh.
d) Thể tích hình nón bằng 1/3 tích của diện tích hình tròn đáy với chiều cao.
e) Diện tích mặt cầu thì bằng 4 lần diện tích hình tròn lớn.
f) Thể tích hình cầu thì bằng 4/3 tích của diện tích hình tròn lớn với bán kính.
Đúng 0
Bình luận (0)
Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy là a, b (a < b) và độ dài đường sinh là l (a, b, l có cùng đơn vị đo).
Áp dụng công thức tính diện tích xung quanh hình nón cụt ta có:
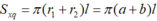
Đúng 0
Bình luận (0)
Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy là a, b (a < b) và độ dài đường sinh là l (a, b, l có cùng đơn vị đo).
Áp dụng công thức tính diện tích xung quanh hình nón cụt ta có:
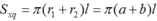
Đúng 0
Bình luận (0)









