Phần ảo của số phức z = ( 1 + i ) 3 là
A. 3 3
B. - 3 3
C. -8i
D. -8
Những câu hỏi liên quan
Phần thực và phần ảo của số phức z = (3 + 4i)(4 - 3i) + (2 - i)(3 + 2i) là
A. 32 và 8i
B. 32 và 8
C. 18 và -14
D. 32 và -8
Phần thực và phần ảo của số phức z thỏa mãn z = ( 1 + 2 i ) 2 + ( 1 - 2 i ) 3 là
A. 14 và 6i
B. –14 và 6
C. 14 và – 6
D. –14 và –6
Ta có:
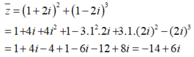
Suy ra z = -14 - 6i. Vậy phần thực và phần ảo của z là: -14 và - 6
Chọn D
Đúng 0
Bình luận (0)
Cho số phức z = 1 + 2 i 2 - i . Phần thực và phần ảo của số phức w = (z + 1)(z + 2) là
A. 2 và 1
B. 1 và 3
C. 2 và i
D. 1 và 3i
Ta có
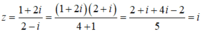
Suy ra w = (z + 1)(z + 2) = (i + 1)(i + 2) = -1 + 2i + i + 2 = 1 + 3i
Chọn B
Đúng 0
Bình luận (0)
Phần thực và phần ảo của số phức z thỏa mãn (1 - i)z - 1 + 5i = 0 là
A. 3 và –2
B. 3 và 2
C. 3 và – 2i
D. 3 và 2i
Ta có: (1 - i)z - 1 + 5i = 0 ⇔ (1 - i)z = 1 - 5i
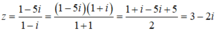
Vậy phần thực và phần ảo của z là 3 và -2
Chọn A
Đúng 0
Bình luận (0)
Cho số phức z = -1 + 3i. Phần thực, phần ảo của z là
A. -1 và 3
B. -1 và -3
C. 1 và -3
D. -1 và -3i
Ta có z = -1 + 3i => z = - 1 - 3 i
Vậy phần thực và phần ảo của z− là -1 và -3.
Chọn đáp án B.
Đúng 0
Bình luận (0)
Phần ảo của số phức z = -1 là
A. -i
B. 1
C. -1
D. 0
Ta có: z= -1 = -1 + 0.i nên phần ảo của số phức z = -1 là 0
Chọn D
Đúng 0
Bình luận (0)
Cho số phức \(z=1-i+i^3\) . Tìm phần thực a và phần ảo b của z:
A: a=1,b=0
B: a=0,b=1
C: a=1,b=-2
D: a=-2,b=1
\(z=1-i+i.i^2=1-i+\left(-1\right).i=1-2i\)
phần thực a=1, phần ảo b=-2
vậy chọn C
Đúng 0
Bình luận (0)
Phần thực và phần ảo của số phức
z
(
1
+
3
i
)
2
là A. 1 và 3 B. 1 và -3 C. -2 và
2
3
D. 2 và
-
2
3
Đọc tiếp
Phần thực và phần ảo của số phức z = ( 1 + 3 i ) 2 là
A. 1 và 3
B. 1 và -3
C. -2 và 2 3
D. 2 và - 2 3
Ta có: z = 1 + 2 3 + 3 i 2 = - 2 + 2 3 i
Vậy phần thực và phần ảo của z là -2 và 2 3
Chọn C
Đúng 0
Bình luận (0)
Cho z = 1 + 2i . Phần thực và phần ảo của số phức w = 2 z + z là
A. 3 và 2
B. 3 và 2i
C. 1 và 6
D. 1 và 6i
Ta có: w = 2 z + z = 2 ( 1 + 2 i ) + ( 1 - 2 i ) = 3 + 2 i
Vậy phần thực của w là 3, phần ảo của w là 2
Chọn A
Đúng 0
Bình luận (0)