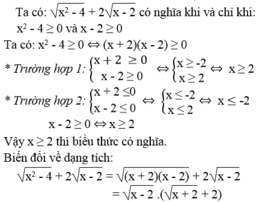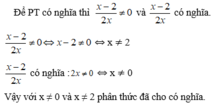Tìm điều kiện của các biến để các phân thức sau có nghĩa 5 x 2 25 x 2 - 10 x y + y 2
Những câu hỏi liên quan
Tìm điều kiện của các biến để các phân thức sau có nghĩa - 5 3 x x - 1 - 2
Tìm điều kiện của các biến để các phân thức sau có nghĩa 2 x 2 + x - 3 x 2 + 5 x + 4
Để phân thức có nghĩa:
x 2 + 5 x + 4 ≠ 0
⇔ (x + 4)(x + 1) ≠ 0
⇔ x ≠ -4, x ≠ -1
Vậy điều kiện để phân thức xác định là x ≠ -4 và x ≠ -1
Đúng 0
Bình luận (0)
Tìm điều kiện của các biến để các phân thức sau có nghĩa - 5 x + 2 3 x + 2 2 x - 1 - 1
Để phân thức xác định ta có: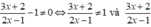 
có nghĩa:
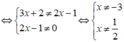
Vậy với x ≠ -3 và x ≠ ½ thì phân thức đã cho được xác định
Đúng 0
Bình luận (0)
Tìm điều kiện của x để các biểu thức sau có nghĩa và biến đổi chúng về dạng tích: x 2 - 4 + 2 x - 2
Tìm điều kiện của các biến để các phân thức sau có nghĩa 3 x 2 - 9 y 2
Điều kiện để phân thức xác định là:
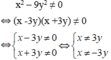
Vậy với x ≠ 3y và x ≠ -3y thì phân thức đã cho có nghĩa
Đúng 0
Bình luận (0)
Tìm điều kiện của các biến để các phân thức sau có nghĩa 3 x - 5 x - 2 2 x
Tìm điều kiện của các biến để các phân thức sau có nghĩa x 2 + 3 x 2 + 3 x - 4
Để phân thức có nghĩa:
x 2 + 3 x – 4 ≠ 0
⇔ (x + 4)(x – 1) ≠ 0
⇔ x ≠ -4 và x ≠ 1
Vậy điều kiện để phân thức có nghĩa là x ≠ - 4 và x ≠ 1
Đúng 0
Bình luận (0)
Tìm điều kiện để các phân thức sau có nghĩa và tìm mẫu thức chung của chúng:
b, x / 4 + 2a , y / 4 - 2a , z / 4 - a^2
\(\dfrac{x}{4+2a}\) có nghĩa khi \(a\ne-2\)
\(\dfrac{y}{4-2a}\)có nghĩa khi \(a\ne2\)
\(\dfrac{z}{4-a^2}\)có nghĩa khi \(a\ne\pm2\)
MTC: \(2\left(2+a\right)\left(2-a\right)\)
Đúng 0
Bình luận (0)
26 tháng 10 2023 lúc 19:58
Tìm điều kiện x để các biểu thức sau có nghĩa
\(\sqrt{x-5}\) \(\dfrac{1}{\sqrt{3x-2}}\)
`sqrt(x-5)` có nghĩa khi:
`x-5 ≥0`
`=> x ≥5`
Vậy `x≥5` thì `sqrt(x-5` có nghĩa
____________
`1/(sqrt(3x-2))` có nghĩa khi
`1/(sqrt(3x-2)) ≥0`
`⇒ 3x-2≥0`
` ⇒3x≥2`
` ⇒x≥2/3`
Vậy `x ≥2/3` thì `1/(sqrt(3x-2))` có nghĩa
Đúng 2
Bình luận (1)