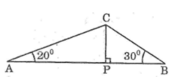
Tam giác ABC có ∠ A = 20 ° , ∠ B = 30 ° , AB = 60cm. Đường vuông góc kẻ từ C đến AB cắt AB tại P. Hãy tìm: CP
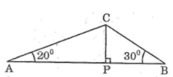
Tam giác ABC có ∠ A = 20 ° , ∠ B = 30 ° , AB = 60cm. Đường vuông góc kẻ từ C đến AB cắt AB tại P. Hãy tìm: AP, BP
Thay CP = 13,394 vào (1) ta có:
AP = 13,394.cotg 20 ° ≈ 36,801 (cm)
Thay CP = 13,394 vào (2) ta có:
BP = 13,394.cotg 30 ° ≈ 27,526 (cm)
cho tam giác ABC đường cao CP. Biết AB= 60cm góc A= 20 độ, góc B= 30 ĐỘ . tính AP, BP ,CP
trong tam giac ABH co\(AH=AB\cdot\sin B\) \(\Rightarrow AH=60\cdot\sin30=30\)
trong tam giac AHC co \(\sin C=\frac{AH}{AC}\Rightarrow AC=\frac{30}{\sin130}\approx39\)(vi \(gocC=180-20-30=130\)
TRONG TAM GIAC APC CO\(PC=AC\cdot\sin A=39\cdot\sin20\approx13,34\)
\(AP=\cos A\cdot39\approx36,65\)
\(\Rightarrow AP+BP=AB\Rightarrow BP=60-36.65=23.35\)
cho tam giác ABC có góc B và góc C lần lượt là 20o và 30o, AB=60cm. Đường vuông góc kẻ từ C đến AB cắt AB tại P.
a) Tính AP; BP
b) Tính CP
Tính góc A (= 130 độ ). tam giác ACP vuông tại P => AP = cot A .CP (1)
tam giác BCP vuông tại P => BP = cot B . CP (2)
(1) +(2) => AP + BP =cot A .CP +cot B . CP
<=> AB = CP( cot A + cot B)
<=>60= CP ( cot 130 + cot 20 )
=> CP xấp xỉ 31.4
từ đó có thể dễ dàng tính ra AP và BP
Cho tam giác ABC có góc B= 20 độ, góc C= 30 độ, AH là đường cao, BC= 60cm. Tính diện tích tam giác ABC (làm tròn đến chữ số thập phân số hai).![]()
Ta có: HB + HC = BC
=>HC = 60 - HB (cm)
Xét △AHC vuông tại H có: \(tan\widehat{C}=\dfrac{AH}{HC}\Rightarrow tan30^0=\dfrac{AH}{HC}\Rightarrow HC=\dfrac{AH}{tan30^0}\left(cm\right)\) (1)
Xét △AHB vuông tại H có: \(tan\widehat{B}=\dfrac{AH}{HB}\Rightarrow tan20^0=\dfrac{AH}{60-HC}\Rightarrow tan20^0\left(60-HC\right)=AH\) (2)
Thay (1) vào (2) ta được: \(\Rightarrow tan20^0\left(60-\dfrac{AH}{tan30^0}\right)=AH \)
\(\Rightarrow tan20^0\left(\dfrac{60.tan30^0}{tan30^0}-\dfrac{AH}{tan30^0}\right)=AH\)
\(\Rightarrow tan20^0\left(\dfrac{60.tan30^0-AH}{tan30^0}\right)=AH\)
\(\Rightarrow tan20^0\left(60.tan30^0-AH\right)=AH.tan30^0\)
\(\Rightarrow tan20^0\left(20\sqrt{3}-AH\right)=AH.tan30^0\)
\(\Rightarrow tan20^0.20\sqrt{3}-AH.tan20^0=AH.tan30^0\)
\(\Rightarrow tan20^0.20\sqrt{3}=AH.\left(tan30^0+tan20^0\right)\)
\(\Rightarrow AH=\dfrac{tan20^0.20\sqrt{3}}{tan30^0+tan20^0}\approx13,3943\left(cm\right)\)
Diện tích của △ABC là: \(S_{ABC}=\dfrac{AH.BC}{2}=\dfrac{13,3943.60}{2}\approx401,83\left(cm^2\right)\)
Vậy...........
CHO TAM GIÁC ABC CÓ \(\widehat{B}=20\)ĐỘ; \(\widehat{C}=30\)ĐỘ; \(BC=60cm\).TÍNH DT TAM GIÁC ABC
Tam giác ABC có \(\widehat{A}=20^0,\widehat{B}=30^0;AB=60cm\). Đường vuông góc kẻ từ C đến AB cắt AB tại P (h.33)
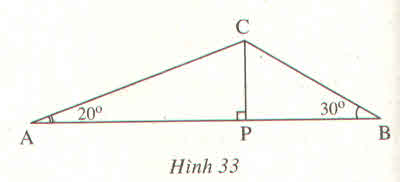
Hãy tìm :
a) AP, BP
b) CP
Đặt AP=x suy ra BP=60-x.Ta có phương trình
xtg\(20^0\)=(60-x)tg\(30^0\)
Đ/s:AP ≈36,801cm;BP=23,119cm;CP=13,396cm
Tham khảo nha
CHO TAM GIÁC ABC CÓ \(\widehat{B}=20\)ĐỘ\(;\) \(\widehat{C}=30\)ĐỘ\(;\)\(BC=60cm\).TÍNH DT TAM GIÁC ABC
cho tam giác ABC vuông tại A với AB=6,AC=8 có đườn cao AH
a. tính HB,HC,HA
b. tính góc B,C
Cho tam giác ABC có góc vuông Ạ,Ab=60cm ,Ác=80cm.Lấy D trên AB sao choAD= 20 cm,Lấy E trên BC sao cho ADEC là hình thang.
a,Tinh dien tich tam giac AEC
b, Tinh dien tich tam giac BED